Wolfram Language™

Das Zipfsche Gesetz

Das Zipfsche Gesetz besagt, dass die Häufigkeit eines Wortes im Korpus einer Sprache umgekehrt proportional zu dessen Rangfolge ist. Dieses Beispiel illustriert mithilfe der neuen Funktionen WordCount und WordCounts das Gesetz mit Wörtern, die in Miguel de Cervantes' Roman Don Quixote vorkommen.

ExampleData enthält den spanischen Text des ersten Bands von Don Quixote.

In[1]:=

textSpanish = ExampleData[{"Text", "DonQuixoteISpanish"}];

Das Beispiel umfasst mehr als 180.000 Wörter.

In[2]:=

WordCount[textSpanish]

Out[2]=

Das Vorkommen jedes einzelnen Wortes wird durch WordCounts als Assoziation gegeben. Das Ergebnis ist bereits in absteigender Reihenfolge sortiert.

In[3]:=

association = WordCounts[textSpanish];

In[4]:=

Take[association, 10]

Out[4]=

Ermitteln Sie die Häufigkeit der 1000 häufigsten Wörter.

In[5]:=

counts = Take[Values@association, 1000];

Um diese Häufigkeiten mit einem Potenzgesetz anzunähern, ermitteln Sie Logarithmen zur linearen Modellanpassung. Das Zipfsche Gesetz besagt, dass der Exponent bei -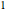 liegen soll, und das Ergebnis liegt nahe an diesem Wert.

In[6]:=

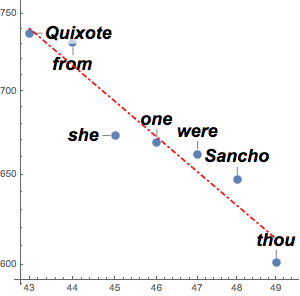
f[x_] = Fit[Log[Transpose[{Range[1000], counts}]], {1, x}, x]

Out[6]=

Visualisieren Sie das Modell gemeinsam mit den Daten.

In[7]:=

Show[ ListLogLogPlot[counts, PlotStyle -> PointSize[0.02]], LogLogPlot[Exp[f[Log[x]]], {x, 1, 1000}, PlotStyle -> Directive[DotDashed, Red]], AspectRatio -> 1, PlotRange -> All ]

Out[7]=

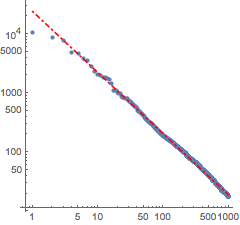
Das Zipfsche Gesetz bewahrheitet sich in jeder Sprache. Daher wird dieselbe Berechnung nun auch mit der englischen Version von Don Quixote durchgeführt.

In[8]:=

textEnglish = ExampleData[{"Text", "DonQuixoteIEnglish"}];

In[9]:=

associationEnglish = WordCounts[textEnglish]; countsEnglish = Take[Values@associationEnglish, 1000];

In[10]:=

Take[associationEnglish, 10]

Out[10]=

Auch hier liegt der gefundene Exponent nahe bei .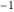

In[11]:=

Fit[Log[Transpose[{Range[1000], countsEnglish}]], {1, x}, x]

Out[11]=