L'Équation du temps

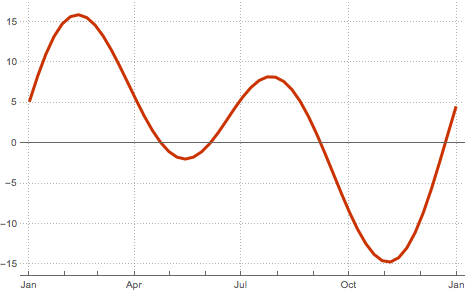
En raison de l'excentricité de l'orbite de la Terre et de l'inclinaison de l'axe de la Terre par rapport au plan de l'orbite, le mouvement apparent du Soleil varie tout au long de l'année. Ceci induit une variation du temps mesuré par une horloge solaire (heure solaire apparente) par rapport à une horloge plus précise, par exemple, celle déterminée par la rotation apparente des étoiles fixes (temps sidéral). Cette différence est connue comme l'Équation du temps.

SiderealTime renvoie des valeurs de temps sidéral en quantités mixtes unitaires, en utilisant MixedUnit.

In[1]:=

SiderealTime[]

Out[1]=

In[2]:=

SiderealTime[]; QuantityUnit[%]

Out[2]=

Un temps sidéral est en fait un angle, et par conséquent, il peut être converti en d'autres unités angulaires.

In[3]:=

UnitConvert[SiderealTime[], "AngularDegrees"]

Out[3]=

L'Équation du temps est déterminée par le mouvement du Soleil, comme donné par SunPosition. Calculez les valeurs hebdomadaires à midi GMT.

In[4]:=

dates = DateRange[ DateObject[{2015, 1, 1}, TimeObject[{12, 0}, TimeZone -> 0], TimeZone -> 0.`], DateObject[{2015, 12, 31}, TimeObject[{12, 0}, TimeZone -> 0], TimeZone -> 0.`], 7];

In[5]:=

sunpos = SunPosition[GeoPosition[{0, 0}], dates, CelestialSystem -> "Equatorial"]

Out[5]=

Utilisez SiderealTime pour calculer l'ascension droite au méridien de Greenwich pour les mêmes dates hebdomadaires.

In[6]:=

stime = SiderealTime[GeoPosition[{0, 0}], dates]

Out[6]=

Enfin, trouvez les valeurs correspondantes de l'Équation du temps en tant que différence entre l'ascension droite du Soleil et le temps sidéral à midi tout au long de l'année. Exprimez le résultat en minutes.

In[7]:=

equationoftime = UnitConvert[(TimeSeriesMap[First, sunpos] - stime), "MinutesOfRightAscension"]

Out[7]=

Les valeurs absolues de l'Équation du temps peuvent être supérieures à 15 minutes.

In[8]:=

MinMax[equationoftime]

Out[8]=

In[9]:=

DateListPlot[equationoftime, GridLines -> Automatic, Axes -> True, PlotTheme -> "Web"]

Out[9]=