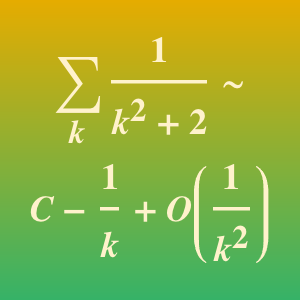Approximez la séquence du nombre d'involutions (AsymptoticRSolveValue)
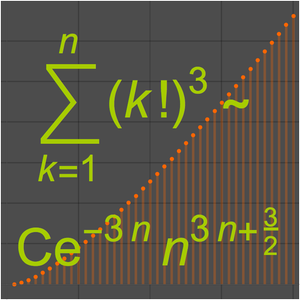
Une involution est une permutation qui est son propre inverse. Dans l'exemple suivant, l'équation différentielle pour la séquence 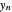 du nombre d'involutions agissant sur
du nombre d'involutions agissant sur 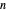 éléments est obtenue en utilisant la fonction FindSequenceFunction. Une approximation asymptotique est ensuite calculée en utilisant une valeur initiale inexacte de
éléments est obtenue en utilisant la fonction FindSequenceFunction. Une approximation asymptotique est ensuite calculée en utilisant une valeur initiale inexacte de 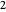 dans la fonction AsymptoticRSolveValue. La formule hybride symbolique-numérique qui en résulte donne une excellente approximation pour le 1000 ème terme de la séquence.
dans la fonction AsymptoticRSolveValue. La formule hybride symbolique-numérique qui en résulte donne une excellente approximation pour le 1000 ème terme de la séquence.
Définissez une fonction pour savoir si une permutation est son propre inverse et est, par conséquent, une involution.
Calculez le nombre d'involutions sur 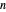 éléments, pour
éléments, pour 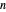 allant de 1 à 10.
allant de 1 à 10.
Utilisez la fonction FindSequenceFunction pour obtenir la relation de récurrence de la séquence.
Obtenez les termes principaux du développement asymptotique.
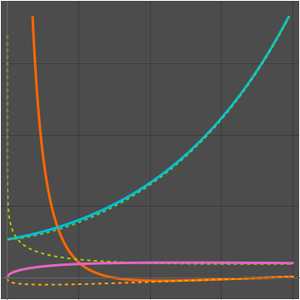
Comparez les valeurs approximatives et réelles.