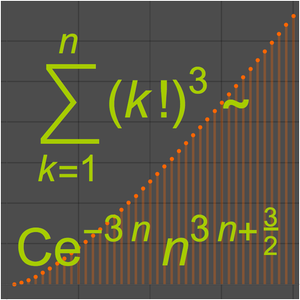
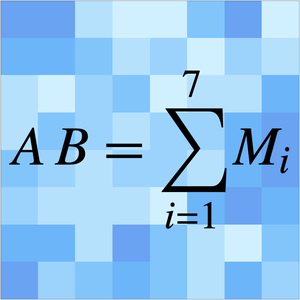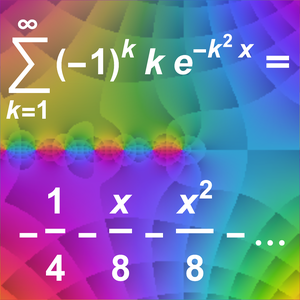Approximate the Sequence of Involution Counts (AsymptoticRSolveValue)
An involution is a permutation that is its own inverse. In the following example, the difference equation for the sequence  of the number of involutions acting on
of the number of involutions acting on  elements is obtained using FindSequenceFunction. An asymptotic approximation is then computed by using an inexact initial value at
elements is obtained using FindSequenceFunction. An asymptotic approximation is then computed by using an inexact initial value at  in AsymptoticRSolveValue. The resulting hybrid symbolic-numeric formula gives an excellent approximation for the 1000 th term of the sequence.
in AsymptoticRSolveValue. The resulting hybrid symbolic-numeric formula gives an excellent approximation for the 1000 th term of the sequence.
Define a function testing if a permutation is its own inverse and is thus an involution.
Compute the number of involutions on  elements for
elements for  from 1 to 10.
from 1 to 10.
Use FindSequenceFunction to obtain the recurrence relation for the sequence.
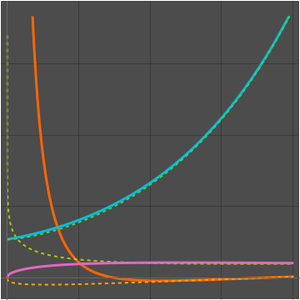
Obtain the leading terms in the asymptotic expansion.
Compare the approximate and actual values.