Compare algoritmos usando relaciones asintóticas
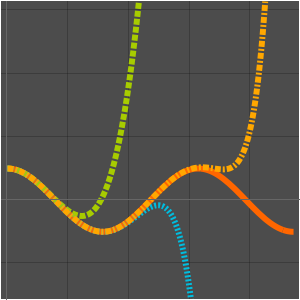
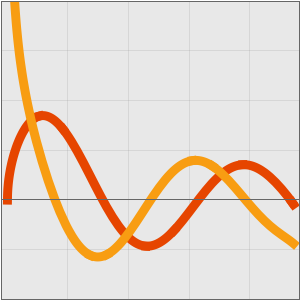
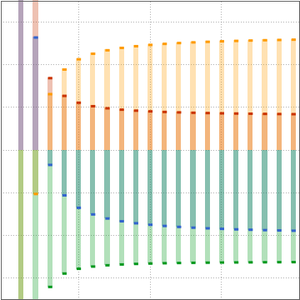
En complejidad computacional, los algoritmos son clasificados por su comportamiento para grandes entradas, típicamente se consideran estar en el infinito. Dos algoritmos comparados según si el tiempo de ejecución de uno es AsymptoticLessEqual (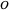 grande), AsymptoticLess (
grande), AsymptoticLess (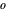 pequeña), AsymptoticGreaterEqual (
pequeña), AsymptoticGreaterEqual (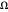 grande), o AsymptoticGreater (
grande), o AsymptoticGreater (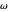 pequeña) el tiempo de ejecución del otro.
pequeña) el tiempo de ejecución del otro.
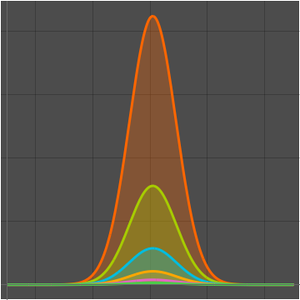
El problema del vendedor ambulante (TSP, en inglés) consiste en encontrar la ruta más corta que conecte 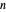 ciudades. Un algoritmo ingenuo probaría todas las rutas
ciudades. Un algoritmo ingenuo probaría todas las rutas 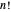 . El algoritmo Held–Karp mejora esto en aproximadamente
. El algoritmo Held–Karp mejora esto en aproximadamente 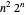 pasos. Muestre que
pasos. Muestre que 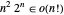 y el algoritmo Held–Karp es más rápido.
y el algoritmo Held–Karp es más rápido.
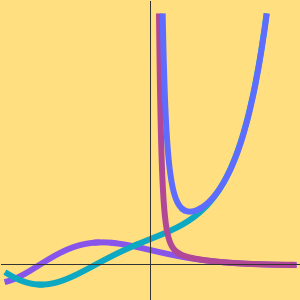
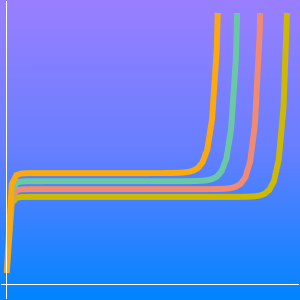
Ambos algoritmos muestran que la clase de complejidad del TSP no es peor que EXPTIME, los cuales son problemas que pueden ser resueltos en tiempo 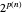 . Por ejemplo,
. Por ejemplo, 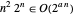 para cualquier
para cualquier 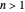 , así que el algoritmo Held-Karp tiene un tiempo de ejecución exponencial.
, así que el algoritmo Held-Karp tiene un tiempo de ejecución exponencial.
Para la función factorial un exponencial lineal no es suficiente porque 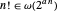 .
.
Sin embargo, un factorial todavía tiene tiempo de ejecución exponencial porque 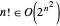 .
.
Soluciones aproximadas pueden ser encontradas en tiempo 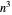 , así que el TSP aproximado en la clase compleja P de problemas solubles en tiempo de polinomio. Cualquier algoritmo de polinomio es más rápido que un exponencial o
, así que el TSP aproximado en la clase compleja P de problemas solubles en tiempo de polinomio. Cualquier algoritmo de polinomio es más rápido que un exponencial o 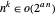 .
.