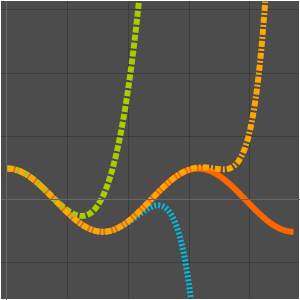
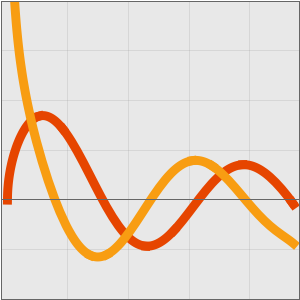
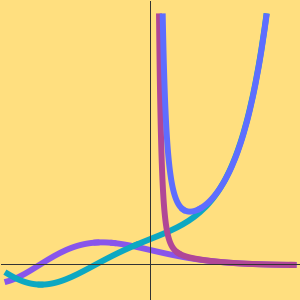
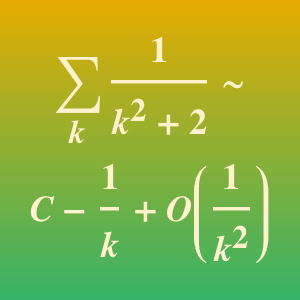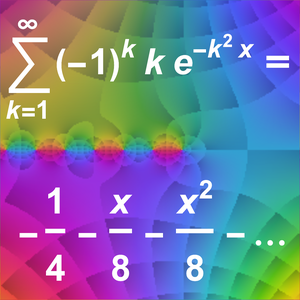Verifique aproximações assintóticas

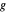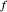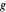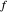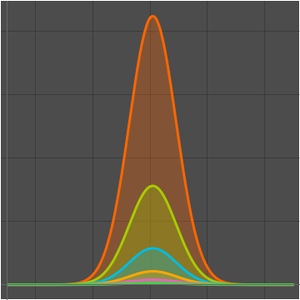
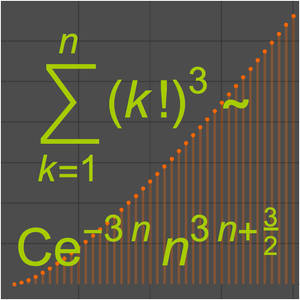
Se uma função aproxima uma função com um erro relativo que desaparece quando se aproxima do ponto base, então é dito ser AsymptoticEquivalent para , normalmente escrito como 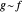. Um exemplo clássico é a aproximação de Stirling à função fatorial.

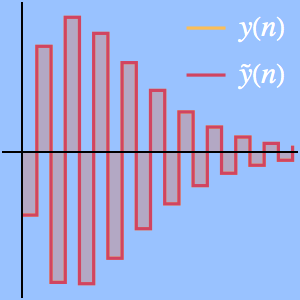
Como o erro relativo vai para zero, o quociente entre as funções vai para .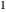

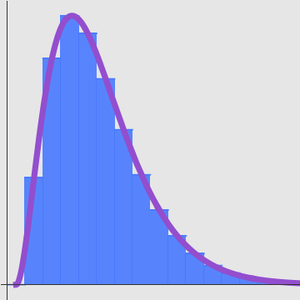
A aproximação de Stirling é surpreendente porque enquanto o erro relativo vai para zero, o erro absoluto vai para o infinito.

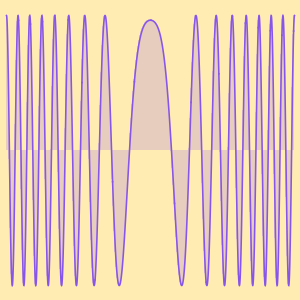
As séries de Taylor fornecem aproximações assintóticas.

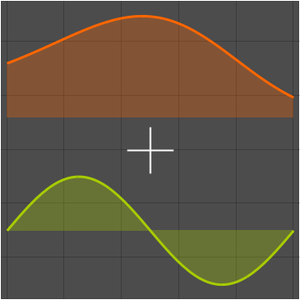
As séries de Laurent também dão aproximações assintóticas.

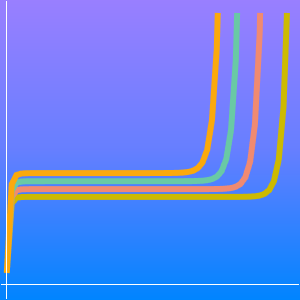
O teorema do número primo estabelece que 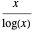é uma aproximação assintótica para a função de contagem de números primos .

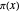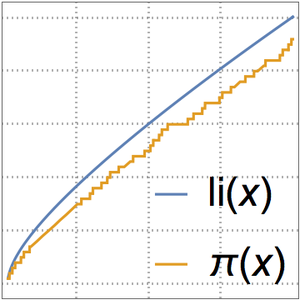
Uma melhor aproximação é dada pela função integral logarítmica .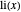

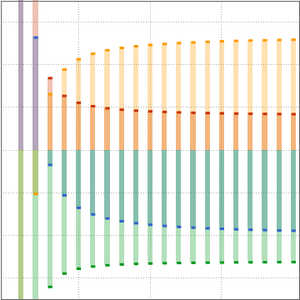
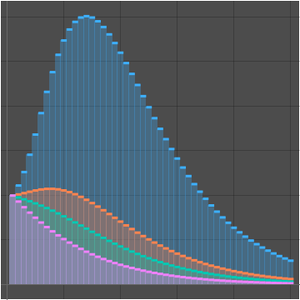
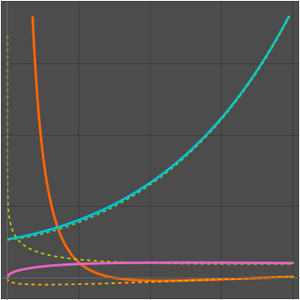
Compare a função de contagem de números primos e as duas aproximações.