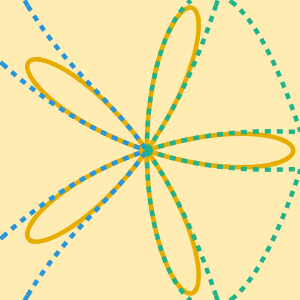
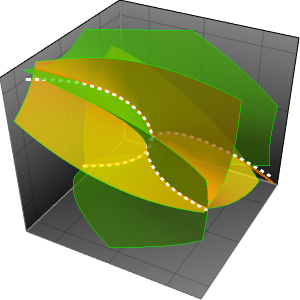
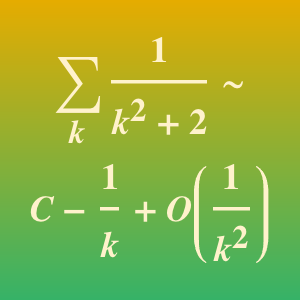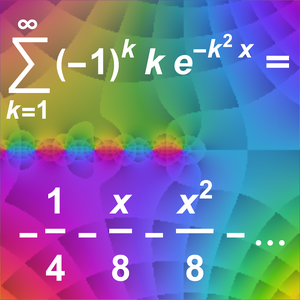Vérifiez les approximations asymptotiques
Si une fonction 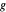 se rapproche d'une fonction
se rapproche d'une fonction 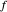 avec une erreur relative qui disparaît à mesure qu'elle s'approche du point de base, alors on dit que
avec une erreur relative qui disparaît à mesure qu'elle s'approche du point de base, alors on dit que  est AsymptoticEquivalent à
est AsymptoticEquivalent à 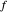 , on le trouve souvent écrit ainsi
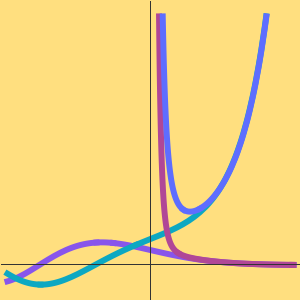
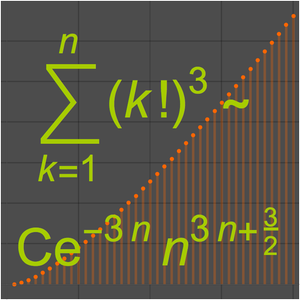
, on le trouve souvent écrit ainsi 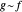 . L'approximation de Stirling de la fonction factorielle est un exemple classique.
. L'approximation de Stirling de la fonction factorielle est un exemple classique.
Puisque l'erreur relative est égale à zéro, le rapport des fonctions est égal à 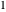 .
.
L'approximation de Stirling est surprenante car si l'erreur relative est égale à zéro, l'erreur absolue tend vers l'infini.
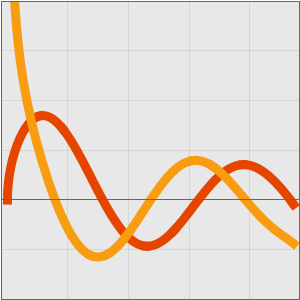
La série de Taylor fournit des approximations asymptotiques.
La série de Laurent fournit aussi des approximations asymptotiques.
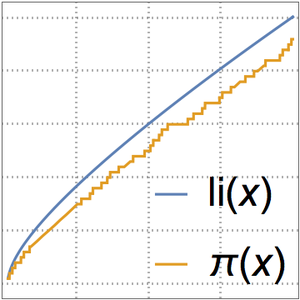
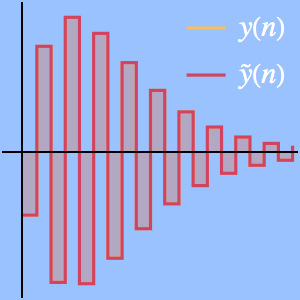
Le théorème des nombres premiers indique que 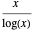 est une approximation asymptotique de la fonction de comptage des nombres premiers
est une approximation asymptotique de la fonction de comptage des nombres premiers 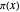 .
.
Une meilleure approximation est donnée par la fonction intégrale logarithmique  .
.
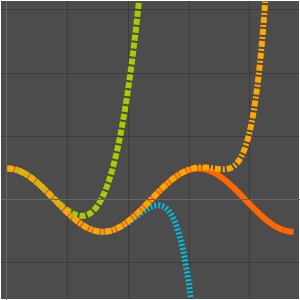
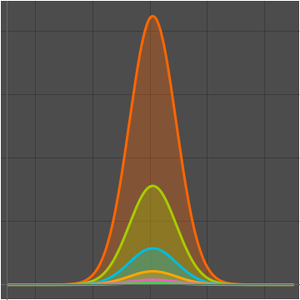
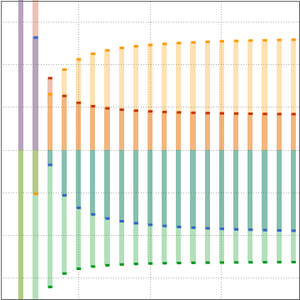
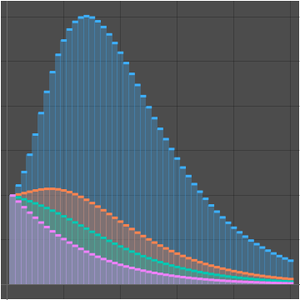
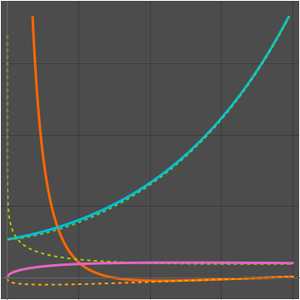
Comparez la fonction de comptage des nombres premiers et les deux approximations.