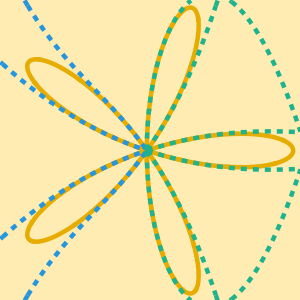
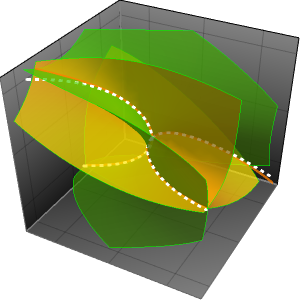
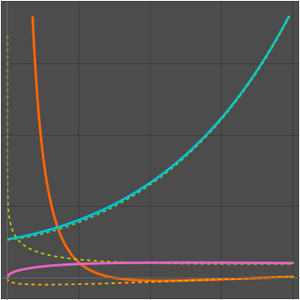
Compare algoritmos usando relações assintóticas
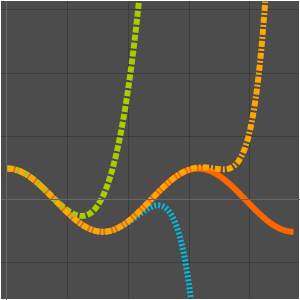
Em complexidade computacional, os algoritmos são classificados por seu comportamento para grandes entradas de dados, tipicamente considerados infinitos. Dois algoritmos são comparados se o tempo de execução de um é AsymptoticLessEqual (big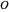 
), AsymptoticLess (little 
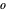), AsymptoticGreaterEqual (big 
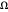) or AsymptoticGreater (little 
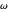) que o tempo de execução de outro.
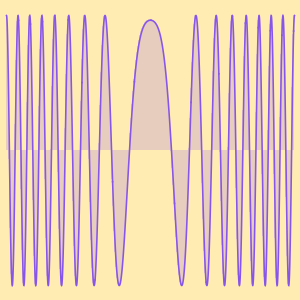
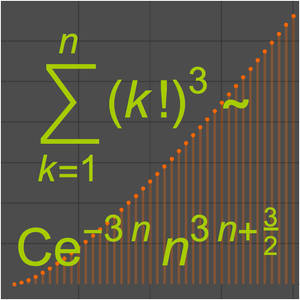
O Problema do caixeiro viajante (PCV) consiste em encontrar a rota mais curta que conecte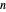 
cidades. Um algoritmo ingênuo tentaria todos as rotas 
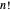. Um algoritmo Held–Karp melhoraria isso em aproximadamente 
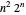passos. Mostre que 
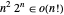e, portanto, que o algoritmo Held-Karp é mais rápido.
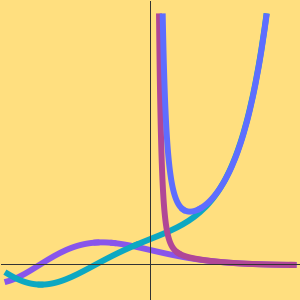
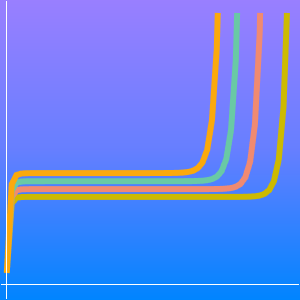
Ambos algoritmos mostram que a classe de complexidade do PCV não é pior que EXPTIME, que são problemas que podem ser resolvidos em tempo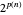 
. Por exemplo, 
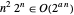para qualquer 
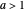, então o algoritmo Held-Karp tem tempo de execução exponencial.
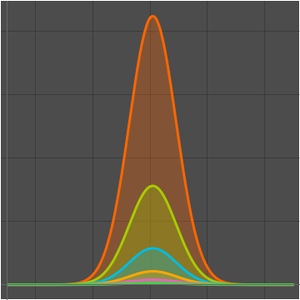
Para a função fatorial, uma exponencial linear não é suficiente porque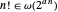 
.
Entretanto, um fatorial ainda tem tempo de execução exponencial porque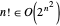 
.
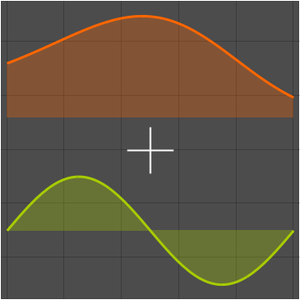
Soluções aproximadas podem ser encontradas em tempo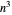 
, então o PCV aproximado está na classe de complexidade P de problemas solúveis em tempo polinomial. Qualquer algoritmo polinomial é mais rápido que um exponencial, ou 
.
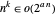