Das Problem des maximalen Schnitts
Der maximale Schnitt zerlegt die Knotenmenge 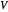 eines Graphen in die Teilmengen
eines Graphen in die Teilmengen 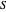 und
und 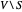 , so dass das Gesamtgewicht
, so dass das Gesamtgewicht 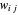 der zwischen den beiden Teilmengen verlaufenden Kanten maximiert wird.
der zwischen den beiden Teilmengen verlaufenden Kanten maximiert wird.
Dieses Beispiel zeigt, wie SemidefiniteOptimization verwendet werden kann, um eine Funktion zu definieren, die eine Variante dieses NP-vollständigen Problems effizient löst.
Angenommen, 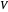 hat
hat 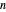 Knoten, so dass sie durch einen Index
Knoten, so dass sie durch einen Index 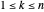 beschrieben werden können.
beschrieben werden können. 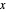 sei ein Vektor mit den Komponenten
sei ein Vektor mit den Komponenten 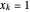 für
für 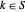 und
und 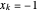 für
für 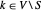 , so dass
, so dass 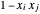 ungleich nur dann null ist (=2), wenn
ungleich nur dann null ist (=2), wenn 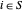 und
und 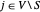 . Somit wird der maximale Schnitt durch Maximierung von
. Somit wird der maximale Schnitt durch Maximierung von 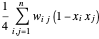 ermittelt, wobei
ermittelt, wobei 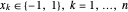 . Die Zielfunktion kann folgendermaßen formuliert werden:
. Die Zielfunktion kann folgendermaßen formuliert werden:
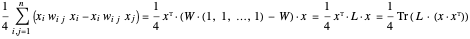
... wobei 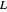 die Laplace-Matrix des Graphen und
die Laplace-Matrix des Graphen und 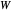 die gewichtete Adjazenzmatrix ist.
die gewichtete Adjazenzmatrix ist.
Bei kleineren Graphen kann das Problem des maximalen Schnitts genau gelöst werden, bei größeren Graphen ist diese Methode jedoch unpraktisch, da das Problem im Allgemeinen eine NP-vollständige Komplexität aufweist.
Das Problem minimiert 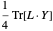 , wobei
, wobei 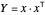 eine symmetrische positive semidefinite Matrix mit Rang 1 ist, mit
eine symmetrische positive semidefinite Matrix mit Rang 1 ist, mit 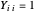 für jedes
für jedes 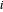 , äquivalent zu
, äquivalent zu 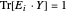 , wobei
, wobei 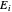 die Matrix mit
die Matrix mit  an der
an der 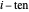 diagonalen Position und 0 überall sonst ist.
diagonalen Position und 0 überall sonst ist.
Um die Lösung praktisch zu gestalten, lösen Sie eine Variante des Problems ohne Rang 1-Bedingung, sodass man nur 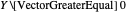 braucht.
braucht.
Die duale Variante des semidefiniten Problems ist gegeben durch
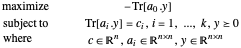
Das Problem wird gelöst mit SemidefiniteOptimization[c, {a0, a1, …, ak}, {"DualMaximizer" }].
Für die Lösung 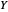 der Relaxation des Problems wird ein Schnitt durch randomisierte Rundung konstruiert: Zerlegen Sie
der Relaxation des Problems wird ein Schnitt durch randomisierte Rundung konstruiert: Zerlegen Sie 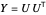 ,
, 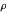 sei ein gleichmäßig verteilter Zufallsvektor der Einheitsnorm und es gilt
sei ein gleichmäßig verteilter Zufallsvektor der Einheitsnorm und es gilt 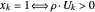 . Zur Veranschaulichung wir eine Funktion definiert, die den "relaxten" Wert, den gerundeten Wert und den Graphen mit den Knoten in
. Zur Veranschaulichung wir eine Funktion definiert, die den "relaxten" Wert, den gerundeten Wert und den Graphen mit den Knoten in 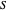 rot darstellt.
rot darstellt.
Ermitteln Sie anhand der oben besprochenen Methode eine Approximation des maximalen Schnitts und vergleichen Sie diese mit dem exakten Resultat.
Ermitteln Sie den maximalen Schnitt eines Gittergraphen.
Ermitteln Sie den maximalen Schnitt eines Zufallsgraphen.
Vergleichen Sie die Rechenzeiten für die Relaxation und den genauen Algorithmus eines Peterson-Diagramms.