最大切割问题
最大切割问题确定图的顶点 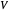 的一个子集
的一个子集 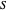 ,从
,从 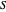 到其补集
到其补集 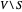 的边的权重
的边的权重 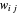 的和被最大化。
的和被最大化。
这个例子演示了如何使用 SemidefiniteOptimization 来设置一个函数,能有效求解 NP 完备的最大切割问题的松弛问题。
假定 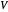 有
有 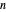 个顶点,可以用索引描述
个顶点,可以用索引描述 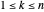 描述。设
描述。设 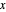 为一个向量,其分量为
为一个向量,其分量为 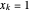 ,
,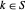 ;
; 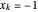 ,
,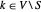 ,只有当
,只有当 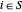 且
且 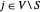 时
时 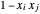 非零 (=2)。因此可通过最大化
非零 (=2)。因此可通过最大化 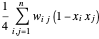 找到最大切割,其中
找到最大切割,其中 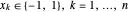 。可将目标函数改写为:
。可将目标函数改写为:
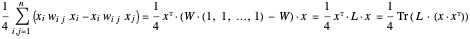
... 其中 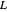 是图的拉普拉斯矩阵,
是图的拉普拉斯矩阵,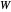 是加权邻接矩阵。
是加权邻接矩阵。
对于简单的问题,可以精确求解最大割问题,但对于较大的图是不切实际的,因为通常问题具有 NP 完备复杂性。
该问题要最小化 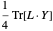 ,其中
,其中 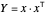 是对称 1 阶半制定矩阵,对于每个
是对称 1 阶半制定矩阵,对于每个 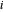 ,
,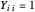 ,等价于
,等价于 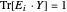 ,其中
,其中 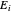 是第
是第 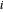 个对角元素为 1、其他位置上的元素为 0 的矩阵。
个对角元素为 1、其他位置上的元素为 0 的矩阵。
为了得到实用解,求解 1 阶条件被排除掉的松弛问题,只要求 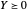 。
。
对偶形式的半定问题如下所示:
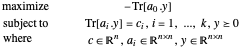
用 SemidefiniteOptimization[c, {a0, a1, …, ak}, {"DualMaximizer" }] 求解。
对于松弛问题的解 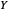 ,通过随机舍入构建切割:分解
,通过随机舍入构建切割:分解 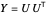 ,令
,令 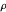 为具有单位范数的均匀分布的随机向量,令
为具有单位范数的均匀分布的随机向量,令 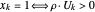 。为了演示,我们定义了一个函数来显示松弛条件下的值、舍入值和图,用红色显示
。为了演示,我们定义了一个函数来显示松弛条件下的值、舍入值和图,用红色显示 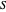 中的顶点。
中的顶点。
用以上所示步骤求近似切割,并与精确结果相比较。
求网格图的最大切割。
求随机图的最大切割。
比较 Peterson 图的松弛算法和精确算法的用时。