Problema de corte máximo
O problema de corte máximo determina um subconjunto 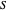 dos vértices
dos vértices 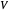 de um grafo, para o qual a soma dos pesos
de um grafo, para o qual a soma dos pesos 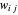 das bordas que se cruzam de
das bordas que se cruzam de 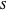 para seus complementos
para seus complementos 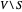 são maximizados.
são maximizados.
Este exemplo monstra como SemidefiniteOptimization pode ser usado para configurar uma função que solucione de forma eficiente uma variante desse problema de corte máximo NP-completo.
Suponha que 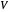 possui
possui 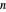 vértices podendo ser descritos por um índice
vértices podendo ser descritos por um índice 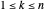 . Use
. Use 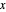 como o vetor com componentes
como o vetor com componentes 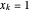 para
para 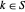 e use
e use 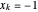 para
para 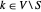 de modo que
de modo que 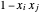 é diferente de zero (=2) apenas se
é diferente de zero (=2) apenas se 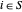 e
e 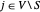 . Assim, o corte máximo é encontrado maximizando
. Assim, o corte máximo é encontrado maximizando 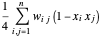 , onde
, onde 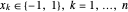 . O objetivo pode ser reescrito como:
. O objetivo pode ser reescrito como:
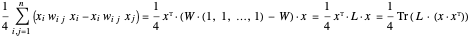
... onde  é a matriz laplaciana do grafo e
é a matriz laplaciana do grafo e 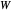 é a matriz de adjacência ponderada.
é a matriz de adjacência ponderada.
Para casos menores, o problema de corte máximo pode ser resolvido com exatidão, mas isso é impraticável para grafos maiores, pois, em geral, o problema tem complexidade NP-completo.
O problema minimiza 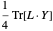 , onde
, onde 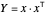 é uma matriz semidefinida positiva de posto 1, com
é uma matriz semidefinida positiva de posto 1, com 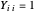 para cada
para cada 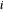 , equivalente a
, equivalente a 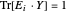 , onde
, onde 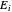 é a matriz com 1 no
é a matriz com 1 no 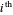 posição diagonal e 0 em todo lugar.
posição diagonal e 0 em todo lugar.
Para tornar a solução prática, resolva um problema relaxado em que a condição de posto 1 é eliminada, para que seja necessária apenas 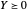 .
.
O problema semidefinido na forma dupla é dado por
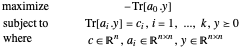
É resolvido usando SemidefiniteOptimization[c, {a0, a1, …, ak}, {"DualMaximizer" }].
Para a solução 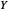 do problema relaxado, um corte é construído por arredondamento aleatório: decomponha
do problema relaxado, um corte é construído por arredondamento aleatório: decomponha 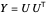 , use
, use 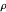 como um vetor aleatório uniformemente distribuído da norma unitária e use
como um vetor aleatório uniformemente distribuído da norma unitária e use 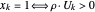 . Para demonstração, é definida uma função que mostra o valor relaxado, o valor arredondado e o gráfico, com os vértices em
. Para demonstração, é definida uma função que mostra o valor relaxado, o valor arredondado e o gráfico, com os vértices em 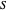 mostrados em vermelho.
mostrados em vermelho.
Encontre um corte máximo aproximado usando o procedimento mostrado anteriormente e compare com o resultado exato.
Encontre o corte máximo de um gráfico de grade.
Encontre o corte máximo para um gráfico aleatório.
Compare os tempos de cálculo para os algoritmos relaxados e exatos para um gráfico de Peterson.