최대 부피 직육면체

볼록 다면체 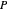에 내접하고 최대 부피의 축 평행의 직육면체를 찾습니다.

이 예는 양수 항의 곱의 최적화를 power-cone 제약 조건으로 나타내는 방법을 설명합니다. 이 제약 조건을 ConicOptimization과 함께 사용하여 최적 조건을 요구할 수 있습니다.

임의의 지점의 볼록 선체로 구축된 임의의 볼록 다면체 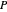를 고려합니다.

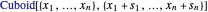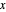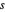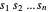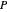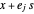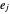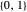직육면체를 Wolfram 언어 로 표현하기 위해 직육면체의 하단 코너점 와 변의 길이 의 벡터를 구합니다. 직육면체의 부피는 변의 길이의 곱이기 때문에, 목적은 을 최대화하는 것입니다. 직육면체의 모든 변이 에 들어갈 수 있으면 직육면체의 점도 모두 맞습니다. 코너는 로 표현될 수 있으며, 여기서 는 에서 가능한 n 튜플(n‐tuples)의 모든 요소의 집합 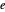에 있습니다.

문제는 다음과 같습니다.

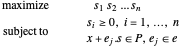
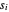는 음수이므로 곱 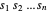을 최대화하는 것은 오목형으로 나타나는 기하 평균 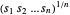을 최대화하는 것과 같습니다. 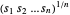을 최대화하는 것은 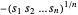볼록형을 최소화하는 것과 같습니다. 보조 변수 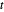를 사용하면 추가 제약 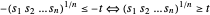를 갖는 선형 목적 함수 -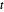에서 이 문제를 다시 공식화 할 수 있습니다.

문제는 다음과 같습니다.

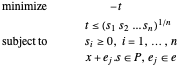
power cone은 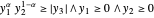이 되는 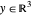의 집합이며, Wolfram 언어의 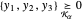으로 나타낼 수 있습니다.

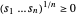이기 때문에, 새로운 제약 조건 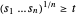는 음수가 아닌 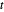에 대해 만족하며, 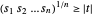와 같습니다. 이것은 다음과 같은 일련의 power cone 제약 조건으로 쓸 수 있습니다.

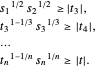
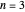일 때, 문제는 다음과 같습니다.

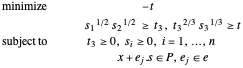
볼록 다면체는 반공간 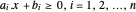의 교차점으로 나타낼 수 있습니다. 각 변의 계수 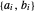을 추출합니다.

문제를 풉니다.

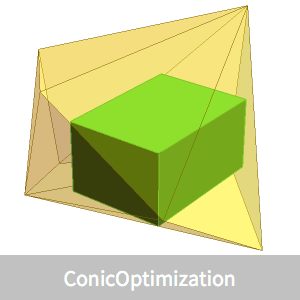
최대 부피의 내접하는 직육면체를 표시합니다.

다면체 대신에 볼록 추로 표현 가능한 집합 K⊆ⁿ(타원체 등)을 취할 수 있습니다. 직육면체의 정점 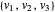는 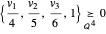일 때, 그리고 그 때에 한하여 타원체의 내부에 있습니다.

문제를 풉니다.

결과를 플롯합니다.