궤도 최적화
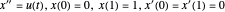을 기준으로 
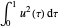를 최소화합니다.
이 예는 변분 문제를 QuadraticOptimization 등의 볼록 법에 효율적으로 풀리는 유한 최적화로 이산화하는 방법을 설명합니다.
변분 문제는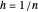 
(
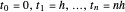)일 때, 구간 [0,1]의 균등한 간격의 격자에서 적분하기 위해 경계값 문제를 이산화하고 사다리꼴 규칙을 사용하여 근사됩니다.
변수 u[i]가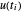 
를, x[i]가 
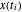를 냅니다. 여기서 
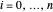입니다.
미분 방정식의 제약 조건은 중앙 이차 차분 근사(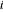
는 1부터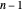 
)를 사용하여 쉽게 표현할 수 있습니다.
경계에서는 제로의 도함수 조건에 따라 가상의 점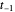 
과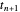 
을 사용할 수 있습니다. 
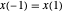과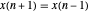 
일 때, 일차 도함수 
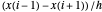에 대한 이차 차분 공식은 
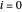과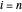 
일 때 제로가 됩니다. 따라서 경계에서는 다음을 사용할 수 있습니다.
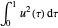의 사다리꼴 공식은 다음과 같이 주어집니다.
사다리꼴 규칙식은 이차식이며 제약 조건은 모든 선형 등식 제약 때문에 이산화된 적분의 최소값은 직접 QuadraticOptimization을 사용하여 구할 수 있습니다.
근사 함수는 Interpolation을 사용하여 구축합니다.
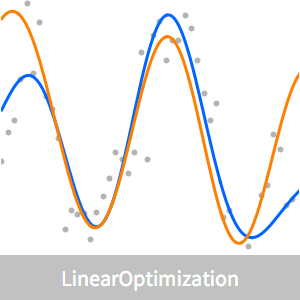
이 문제는 정확하게 해석된 풀이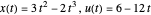 
가 알려져 있기 때문에 이산화의 오차를 그릴 수 있습니다.
점근 오차는 거의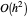 
입니다. 위의 
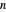을 두 배인 200으로 계산하면 오차는 여기에 표시된 것의 약 1/4이 됩니다.
해석적 해는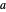 
가 매개 변수인 경우 
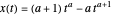의 곡선의 계열을 고려하여 구할 수 있습니다. 이 파라메트릭 곡선은 주어진 경계 조건 
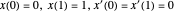을 만족합니다. 
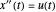이므로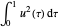 
를 최소화하는 최적 매개 변수 
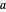를 구할 수 있습니다.
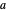의 최적값은 2에서 찾을 수 있으며, 해석적 결과는 
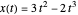입니다.
