최대 컷 문제
최대 절단 문제는 부분 집합 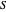 로부터 그 여집합
로부터 그 여집합 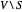 까지를 횡단하는 변의 무게
까지를 횡단하는 변의 무게 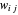 의 총합이 최대가 되는 그래프의 정점
의 총합이 최대가 되는 그래프의 정점 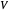 의 부분 집합
의 부분 집합 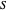 를 구하는 것입니다.
를 구하는 것입니다.
이 예는 SemidefiniteOptimization을 사용하여 NP 완전의 최대 컷 문제의 완화를 효율적으로 해결하는 함수를 설정하는 방법을 보여줍니다.
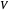 가
가 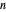 개의 정점을 가지고, 그 정점이 지표
개의 정점을 가지고, 그 정점이 지표 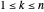 으로 표현됩니다.
으로 표현됩니다. 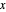 를
를 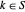 의 경우
의 경우 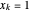 ,
, 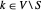 일 때
일 때 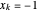 의 요소를 갖고 벡터로
의 요소를 갖고 벡터로 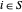 이고,
이고, 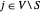 의 경우에만 제로가 아닌(=2)이 되도록 합니다. 그러므로, 최대 하락은
의 경우에만 제로가 아닌(=2)이 되도록 합니다. 그러므로, 최대 하락은 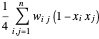 를 최대화함으로써 구해집니다. 여기서
를 최대화함으로써 구해집니다. 여기서 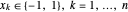 입니다.
입니다.
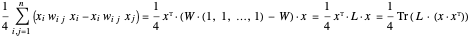
목적은 위와 같이 고쳐 쓸 수 있습니다. 여기서 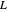 은 그래프의 라플라시안 행렬,
은 그래프의 라플라시안 행렬, 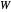 는 가중된 인접 행렬입니다.
는 가중된 인접 행렬입니다.
작은 그래프의 경우 최대 컷 문제는 엄격하게 해결할 수 있지만, 큰 그래프가 되면 일반적으로 문제가 NP 완전성이 포함되기 때문에 실행이 어렵습니다.
이 문제는 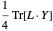 를 최소화합니다. 여기서
를 최소화합니다. 여기서 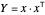 는 랭크-1의 대칭인 양의 준정부호 행렬이며, 각각의
는 랭크-1의 대칭인 양의 준정부호 행렬이며, 각각의 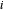 에 대해
에 대해 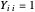 입니다. 이것은
입니다. 이것은 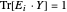 , 여기서
, 여기서 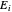 는
는 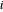 번째 대각선 위치에 1, 다른 위치에 0인 행렬과 동등합니다.
번째 대각선 위치에 1, 다른 위치에 0인 행렬과 동등합니다.
해를 실천하기 위해 완만한 문제를 풀어봅니다. 랭크-1의 조건이 배제되었기 때문에 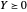 밖에 필요하지 않습니다.
밖에 필요하지 않습니다.
이중 형식의 준정부호의 절반값 문제는 다음과 같습니다.
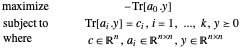
이는 SemidefiniteOptimization[c, {a0, a1, …, ak}, {"DualMaximizer" }]를 사용하여 풉니다.
완화 문제의 해석 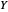 에서 것은 랜덤화된 등근것에 의해 구축됩니다.
에서 것은 랜덤화된 등근것에 의해 구축됩니다. 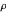 를 단위 노름의 균일 분포에 따라 랜덤 벡터로
를 단위 노름의 균일 분포에 따라 랜덤 벡터로 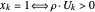 으로
으로 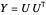 를 분해합니다. 예를 위해 완화값, 반올림 값, 빨간색으로 표시된
를 분해합니다. 예를 위해 완화값, 반올림 값, 빨간색으로 표시된 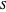 의 정점을 포함하는 그래프를 나타내는 함수가 정의됩니다.
의 정점을 포함하는 그래프를 나타내는 함수가 정의됩니다.
앞서 제시한 방법 사용하여 최대 컷의 근사를 구하고, 정확한 결과와 비교합니다.
격자 그래프의 최대 컷을 구합니다.
랜덤 그래프의 최대 컷을 구합니다.
피터슨 그래프에서 완화 알고리즘과 강력한 알고리즘에 걸리는 시간을 비교합니다.