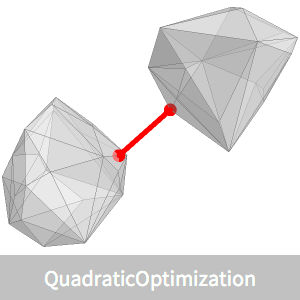
최소 경계 타원체
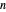차원에서 
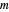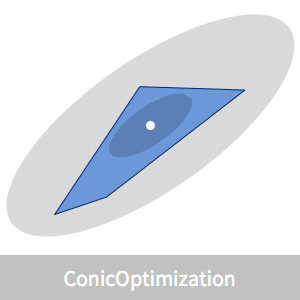
개의 점의 집합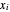 
가 주어 졌을 때, 모든 점을 둘러싸는 최소 부피 타원체인 Löwner-John 타원체를 구합니다.
이 예는 고비선형의 볼록 목적 함수 및 제약 조건으로 표시되는 문제의 경우 NMinimize를 사용하면 볼록 최적화로 쉽게 풀 수 있는 문제로 변환할 수 있음을 보여줍니다.
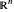의 타원체는 
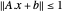인 점 집합 
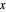에 의해 설명될 수 있습니다. 이 때 
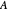는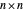 
의 준정부호 행렬, 
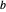는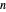 
-벡터입니다. 타원체의 부피는 
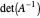에 비례합니다. 
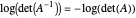는 볼록이며 다음의 해를 찾습니다.
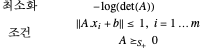
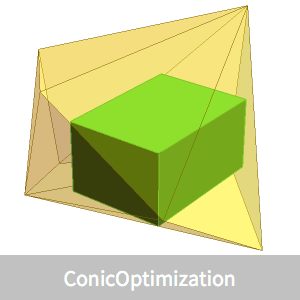
여기에 제시한 예는 시각화 할 수 있도록 삼차원의 임의의 점 집합으로 이루어졌습니다. 해의 알고리즘은 더 큰 차원 
을 처리 할 수 있습니다.
NMinimize를 사용하여 해를 구합니다.
삼차원에서 타원체는 Ellipsoid 그래픽 원시에 의해 설명할 수 있습니다.
BoundingRegion은 둘러싸는 타원체를 빨리 구할 수 있지만 그 타원체의 부피는 커집니다.
