분석의 중심
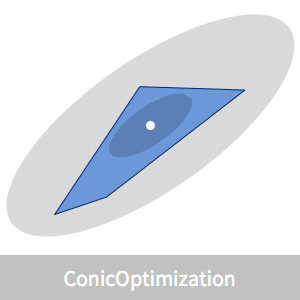
볼록 다각형은 반평면 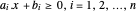 의 교차로 나타낼 수 있습니다. 해석적 중심은 변까지의 거리를 곱한 값을 최대화하는 다각형 내부의 점으로 정의 할 수 있습니다. 다면체 내부의 점
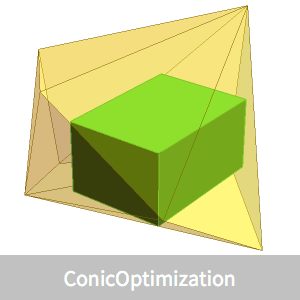
의 교차로 나타낼 수 있습니다. 해석적 중심은 변까지의 거리를 곱한 값을 최대화하는 다각형 내부의 점으로 정의 할 수 있습니다. 다면체 내부의 점 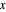 에서 각면까지의 거리는
에서 각면까지의 거리는 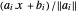 이기 때문에 해석적 중심은
이기 때문에 해석적 중심은 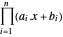 를 극대화하는
를 극대화하는 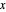 입니다.
입니다.
이 예는 지수 함수적인 원뿔 제약을 ConicOptimization에서 사용하여 해석적 중심을 구하고 LinearOptimization을 사용하여 다각형의 부등식 표현을 추출하는 방법을 보여줍니다.
볼록 다각형을 가져옵니다.
각 변의 계수 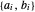 을 추출합니다.
을 추출합니다.
다각형에 대응하는 스칼라 부등식은 다음과 같습니다.
문제를 볼록 최소화로 표현하기 위해 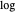 를 취한 목적함수
를 취한 목적함수 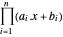 를 부정합니다. 변환된 목적함수는
를 부정합니다. 변환된 목적함수는 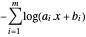 입니다.
입니다.
대수의 합은 오목이며, 그 부정은 볼록이므로 보조 변수 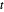 는 제약 조건
는 제약 조건 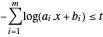 하에서
하에서 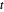 의 목적 함수로 도입됩니다.
의 목적 함수로 도입됩니다.
해석적 중심의 위치를 시각화합니다.
해석적 중심을 중심으로 하여 내접 타원체로 피복 타원체를 주는 간단한 공식이 있습니다.