구조 최적화 문제
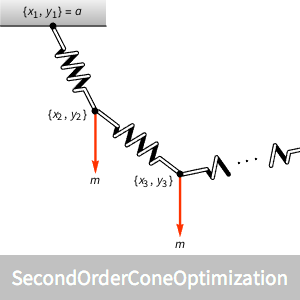
링크의 각 연결 지점에 질량이 있는 여러 개의 스프링 링크로 구성된 매달린 체인의 모양을 구합니다.
이 예는 평형에 대한 최소의 에너지 상태를 이차 원뿔(노름) 제약 조건 하에서 최적화 문제로 나타내는 방법을 보여줍니다. 이것은 SecondOrderConeOptimization으로 쉽게 해결할 수 있습니다.
각 링크의 끝점의 수직 하중 하에서 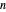 개의 스프링 링크에 의해 형성되는 매달린 체인의 모양을 구합니다. 목적은 양쪽의 위치가
개의 스프링 링크에 의해 형성되는 매달린 체인의 모양을 구합니다. 목적은 양쪽의 위치가 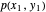 및
및 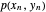 인 경우 링크의 위치
인 경우 링크의 위치 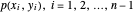 을 구할 수 있습니다.
을 구할 수 있습니다.
스프링의 무게를 무시하고 중력에 의한 포텐셜 에너지는 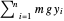 입니다. 여기서
입니다. 여기서 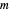 은 각 끝점에서의 수직 하중,
은 각 끝점에서의 수직 하중, 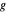 는 표준 중력입니다.
는 표준 중력입니다.
길게 늘려서 걸리는 스프링 링크의 장력에 의한 포텐셜 에너지는 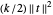 입니다. 여기서
입니다. 여기서 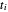 는 스프링 링크
는 스프링 링크 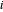 의 늘림,
의 늘림, 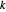 는 스프링의 경도입니다.
는 스프링의 경도입니다. 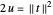 를 사용하면 에너지는
를 사용하면 에너지는 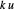 로 변환됩니다.
로 변환됩니다.
이 변환을 위해 추가 제약 조건 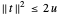 를 더해주어야 합니다.
를 더해주어야 합니다.
연결된 사슬의 끝은 위치 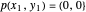 과
과 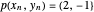 에서 고정됩니다.
에서 고정됩니다.
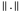 는 볼록이므로 각 스프링이 조건
는 볼록이므로 각 스프링이 조건 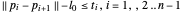 을 만족하는 것만으로 충분합니다. 여기서
을 만족하는 것만으로 충분합니다. 여기서 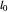 은 스프링의 정지 길이입니다.
은 스프링의 정지 길이입니다.
설계 파라미터는 아래와 같습니다.
최종 목적 함수는 최소화되어야하며 중력과 스프링 포텐셜 에너지의 합입니다.
각 스프링 링크의 끝점을 구합니다.
결과의 스프링 링크의 모양을 시각화합니다.
길게 늘이는 것은 링크 체인의 끝에 있는 링크로 갈수록 커집니다. 링크 11과 12의 늘어남이 가장 작습니다.
해는 링크의 수와 끝점을 조작하기에 충분한 속도입니다.