고윳값 최적화
결합의 고윳값에 대한 다양한 특성을 최적화하는 대칭 행렬의 선형 결합을 구합니다.
이 예는 다양한 형태의 준정부호 제약 조건(실질적으로 고윳값에 대한 제약 조건)을 SemidefiniteOptimization과 함께 사용하여 고유 진동수 최적화 문제를 푸는 방법을 설명합니다.
대칭행렬 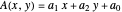 의최대 고윳값을 최소화하는
의최대 고윳값을 최소화하는 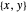 를 구합니다.
를 구합니다.
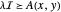 가
가 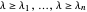 는
는 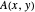 의
의 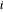
 번째 고윳값과 동일하므로 이 분제는 선형 행렬 부등식을 공식화 할 수 있습니다.
번째 고윳값과 동일하므로 이 분제는 선형 행렬 부등식을 공식화 할 수 있습니다.
최대 고윳값 행렬을 구축합니다.
이것의 고윳값을 계산합니다.
최대 고윳값의 플롯에서 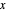 와
와 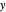 의 함수로 답을 표시합니다.
의 함수로 답을 표시합니다.
몬테카를로 시뮬레이션을 실행하고 결과의 타당성을 검증합니다.
비슷한 문제를 풀어 봅니다. 최소 고윳값을 극대화합니다.
최대 고윳값과 최소 고윳값의 차이를 최소화합니다.
절댓값 고윳값(스펙트럼 노름)에 의해 최대의 고윳값을 최소화합니다.
원칙적으로 이것은 모든 크기의 숫자 행렬을 조합하여 사용할 수 있습니다.