Planificación óptima de superficies
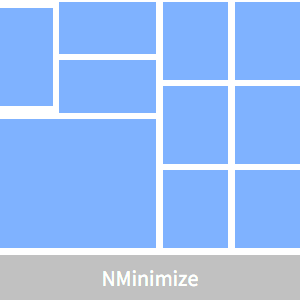
Considere el problema de colocar 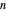 rectángulos más pequeños dentro de un rectángulo más grande de perímetro mínimo con restricciones en la colocación relativa, relación de aspecto, espacio entre los mismos y el área de los rectángulos más pequeños.
rectángulos más pequeños dentro de un rectángulo más grande de perímetro mínimo con restricciones en la colocación relativa, relación de aspecto, espacio entre los mismos y el área de los rectángulos más pequeños.
Este ejemplo demuestra el uso de Wolfram Language para definir una función que usa NMinimize para resolver problemas de planeación de superficies. La función usa desigualdades vectoriales, incluyendo una inequidad semidefinida.
Describa el rectángulo más grande con Rectangle[{0, 0}, {H, W}] y cada uno de los más pequeños con ri=Rectangle[{xi, yi}, {xi+wi, yi+hi}], i=1 … n .
La colocación relativa puede ser descrita por dos grafos dirigidos, uno para la colocación horizontal y el otro para la colocación vertical. Si hay un borde ij, entonces ri debería estar a la izquierda (o debajo) de rj.
Para simplificar, asuma que todos los rectángulos deben tener relación de aspecto entre 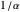 y
y 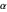 para
para 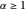 y que el espacio entre los rectángulos es
y que el espacio entre los rectángulos es 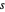 .
.
Con estas entradas y una lista de las áreas de los rectángulos más pequeños, puede definir una función planFloor que encuentre el perímetro mínimo del rectángulo más grande.
Configure los grafos para la colocación relativa de 10 rectángulos más pequeños.
Requiera que las áreas de todos los rectángulos más pequeños sean 100, excepto para uno que tenga un área de 400.
Esto optimiza el plano.
Muestre el plano óptimo.
Esto muestra que la restricción de área cumple con la igualdad.
Compare diseños cuando las áreas se hacen aleatorias.