최적의 평면 계획

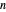개의 작은 직사각형을 최소의 둘레를 가진것 보다 큰 직사각형 안에 배치하는 문제를 생각해 봅니다. 여기서 상대적인 배치, 종횡비, 사이의 간격, 작은 직사각형의 면적에 대한 제약이 있습니다.

이 예는 NMinimize를 사용하는 함수의 정의에 Wolfram 언어를 사용하여 평면 계획 문제를 푸는 것입니다. 이 함수는 준정부호 부등식을 포함한 벡터 부등식을 사용합니다.

큰 사각형을 Rectangle[{0, 0}, {H, W}]에서 작은 사각형을 각각 r_i=Rectangle[{x_i, y_i}, {x_i+w_i, y_i+h_i}], i=1 … n 으로 기술합니다.

상대적 배치는 가로 배치 및 세로 배치의 두 유향 그래프로 나타낼 수 있습니다. 변 ij가 있다면 r_i 는 r_j의 왼쪽(또는 아래쪽)입니다.

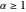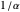간단하게 하기 위해 모든 사각형의 가로 세로 비율은 에서 및 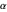사이이며 사각형끼리의 간격은 로 합니다.

이러한 입력과 작은 직사각형의 면적의 목록이 주어지면 최소 둘레를 가진 큰 직사각형을 구하는 함수 planFloor을 정의 할 수 있습니다.

10개의 작은 직사각형의 상대적인 위치에 대한 그래프를 설정합니다.

작은 사각형 중 1개만 면적이 400이고 나머지는 모두 100이 되도록합니다.

다음에 의해 평면 계획을 최적화합니다.

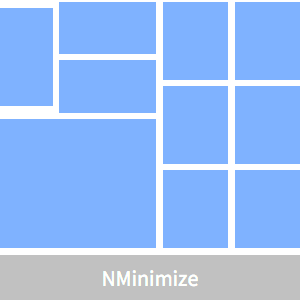
최적의 계획을 표시합니다.

다음은 공간의 제약이 만족되는 것을 보여줍니다.

면적이 랜덤인 경우의 배치를 비교합니다.