Diseño óptimo de entramado
Diseñe un entramado de peso mínimo que esté anclado a la pared en un extremo, y que soporte una carga en el otro extremo.
Este ejemplo demuestra cuántos atributos de Wolfram Language pueden ser usados en conjunto para crear una forma simbólica de un problema de optimización lineal que pueda ser resuelto de forma eficiente usando LinearOptimization.
Seleccione algunas posiciones específicas donde el entramado esté anclado a la pared.
La posición donde la carga se aplica es al extremo del entramado.
El entramado puede ser modelado usando enlaces y nodos. Cada nodo es conectado a un nodo adyacente por medio de un enlace. Aquí presentamos un posible patrón de conectividad.
Los nodos candidatos son colocados en una retícula rectangular.
Visualice las posiciones de los nodos, las posiciones de los puntos de anclaje, la posición donde se aplica la fuerza y la conectividad de un solo nodo en medio del entramado.
Cada nodo está asociado con un índice único. Association proporciona eficientemente una tabla de búsqueda rápida.
Encuentre los índices asociados con los puntos de anclaje y fuerza.
Construya una función que proporcione la conectividad de cualquier punto de retícula para cualquier patrón de conectividad determinado.
Para un nodo 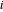 determinado, use la conectividad para determinar los enlaces que incluyen dicho nodo. Si los nodos
determinado, use la conectividad para determinar los enlaces que incluyen dicho nodo. Si los nodos 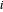 y
y 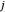 están conectados, entonces
están conectados, entonces 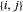 y
y  representan el mismo enlace. Para evitar la repetición, considere solo el nodo con
representan el mismo enlace. Para evitar la repetición, considere solo el nodo con 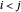 .
.
Describa el conjunto de enlaces por ℒ de manera que si el nodo 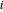 y el nodo
y el nodo 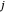 forman un enlace, entonces
forman un enlace, entonces 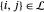 .
.
Asuma que el grosor de un enlace, y por lo tanto la masa por unidad de longitud, requiere ser proporcional a la fuerza que se ejercerá sobre ese enlace. Una manera conveniente de describir los enlaces en ℒ es tener un índice de enlaces de manera que para cada par conectado  , exista un índice único
, exista un índice único 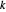 con
con 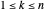 .
.
El objetivo es minimizar 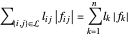 , donde
, donde 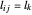 es la longitud del enlace entre los nodos
es la longitud del enlace entre los nodos 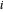 y
y 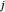 , con índices
, con índices 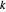 y
y 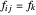 es la fuerza ejercida por el enlace en sus puntos extremos.
es la fuerza ejercida por el enlace en sus puntos extremos.
La función 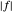 es no lineal, pero puede ser expresada como una función lineal introduciendo
es no lineal, pero puede ser expresada como una función lineal introduciendo 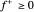 y
y 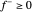 para que
para que 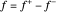 y
y 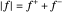 . El objetivo es
. El objetivo es 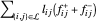 .
.
En cada nodo excepto el punto de fuerza, no hay fuerzas externas aplicadas.
En el punto de fuerza, existe una fuerza unitaria vertical descendiente aplicada.
En cada nodo no anclado 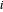 , debe haber un balance de fuerza
, debe haber un balance de fuerza 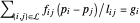 , donde
, donde 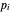 es la posición del nodo
es la posición del nodo 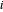 y
y 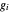 es la fuerza externa en el nodo
es la fuerza externa en el nodo 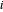 . Defina una función que proporcione la restricción del balance de fuerza para el nodo
. Defina una función que proporcione la restricción del balance de fuerza para el nodo 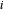 .
.
Use Complement para evitar incluir los nodos de anclaje.
Las restricciones finales son:
Resuelva el sistema resultante.
Visualice el entramado óptimo con tonos en azul indicando la compresión de los enlaces y tonos en rojo indicando la expansión de los enlaces.