最佳桁架设计
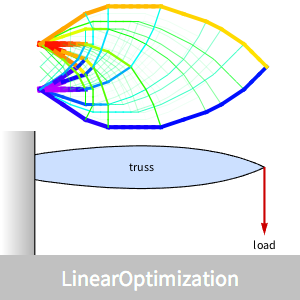
设计一个最小重量的桁架,一端固定在墙上,必须能够承受另一端的负载。
这个例子演示了可以将 Wolfram 语言的多少特征一起使用以形成符号形式的线性优化问题,然后通过 LinearOptimization 高效求解。
选择桁架固定在墙上的几个特定位置。
施加负载的位置在桁架的末端。
可以用 link 和节点对桁架进行建模。每个节点通过 link 连接到相邻节点。这里给出了一种可能的连接模式。
将候选节点放在矩形点阵中。
可视化节点位置、锚点位置、施加力的位置以及桁架中部单个节点的连接性。
每个节点与一个唯一索引关联。Association 提供了一个可高效进行查找的表格。
找到与锚点和着力点相关联的索引。
构建一个函数,提供任一阵点对给定的连接模式的连接性。
对于给定节点 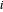 ,用连接性来确定哪些 link 包含该节点。如果节点
,用连接性来确定哪些 link 包含该节点。如果节点 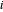 和
和 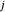 相连,那么
相连,那么 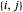 和
和 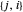 表示相同的 link。为了避免重复,只考虑
表示相同的 link。为了避免重复,只考虑 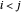 的那一个。
的那一个。
用 ℒ 描述一组 link,如果节点 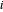 和节点
和节点 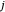 形成一个 link,则
形成一个 link,则 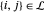 。
。
假设 link 的厚度以及每单位长度的质量需要与将施加在该 link 上的力成比例。描述 ℒ 中的 link 的一种简便方法是对 link 建立索引,使得对应于每对连接 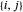 ,有一个唯一的索引
,有一个唯一的索引 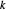 ,
,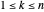 。
。
目标是最小化 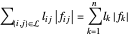 ,其中
,其中 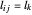 是索引为
是索引为 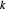 的节点
的节点 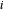 和
和 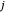 之间的 link 的长度,
之间的 link 的长度,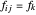 是 link 在末端施加的力。
是 link 在末端施加的力。
函数 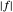 是非线性的,但可以通过引入
是非线性的,但可以通过引入 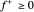 和
和 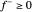 ,使得
,使得 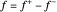 和
和 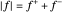 来表示为线性函数。目标函数是
来表示为线性函数。目标函数是 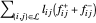 。
。
在除施力点之外的每个节点处不施加外力。
在施力点处,施加垂直向下的单位力。
在每个非锚定节点 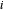 处,要处于力平衡状态
处,要处于力平衡状态 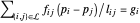 ,其中
,其中 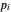 是节点
是节点 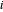 的位置,
的位置,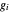 是节点
是节点 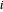 处的外力。定义一个函数,给出节点
处的外力。定义一个函数,给出节点 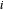 处的力平衡约束条件。
处的力平衡约束条件。
用 Complement 避免将锚点包含在内。
最终的约束条件为:
对所得系统进行求解。
可视化最佳桁架,用蓝色系表示 link 的压缩,用红色系表示 link 的扩展。