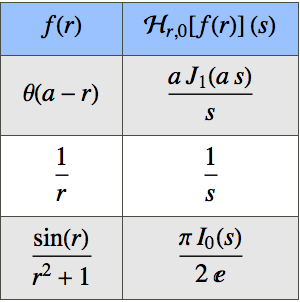Cálculo de la invariante de Klein para una curva elíptica
Las invariantes de las funciones elípticas de Weierstrass son conceptos estándar definidos para curvas elípticas. La versión 12 proporciona funciones para trabajar directamente con estas invariantes, así como los períodos medios y los valores en períodos medios de estas funciones elípticas.
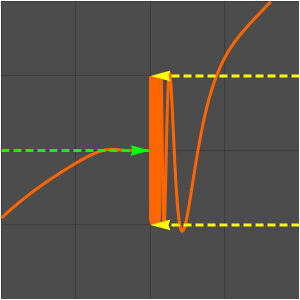
WeierstrassE1, WeierstrassE2 y WeierstrassE3 proporcionan los valores de WeierstrassP el los períodos medios correspondientes.
De manera similar, WeierstrassEta1, WeierstrassEta2 y WeierstrassEta3 proporcionan los valores de WeierstrassZeta en los períodos medios correspondientes.
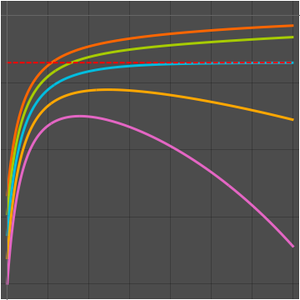
Finalmente, WeierstrassInvariantG2 y WeierstrassInvariantG3 definen las invariantes para las funciones elípticas de Weierstrass, lo cual facilita su uso en ejemplos como el siguiente.
Defina la discriminante de la curva elíptica de Weierstrass.
Calcule la j-invariante de Klein usando las g-invariantes de la curva.
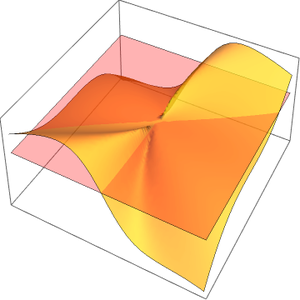
Cree un gráfico de la parte imaginaria de la invariante de Klein.
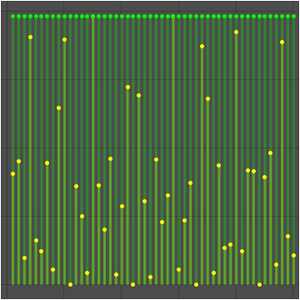
Compare con el valor de función incorporado.