Os recipientes mais eficientes para determinados formatos
O domínio da entidade "Solid" contém regiões fechadas no espaço que são de interesse matemático.
Muitas propriedades estão disponíveis para cada sólido.
Naturalmente, duas dessas propriedades são área de superfície e volume.
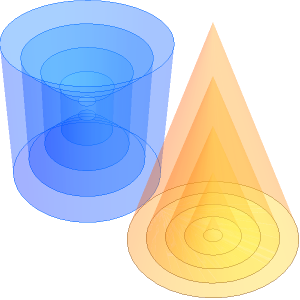
Como é sabido, a proporção da área da superfície em relação ao volume é minimizada em todas as formas possíveis pela esfera preenchida (bola). No entanto, também é interessante considerar os parâmetros que minimizam a área de superfície necessária para incluir um volume fixo para outras famílias de sólidos. Por exemplo, é fácil mostrar que o cilindro sólido que otimiza o seu volume tem uma razão entre a altura e o raio da base de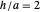 
(ou equivalente a um diâmetro base igual à sua altura).
Você também pode considerar outros sólidos, nos quais, por simplicidade, o volume é fixo à unidade.
De todos os cubóides, o cubo (isto é, cubóide equilateral) fornece o maior volume contido por área de superfície.
Um tetraedro triretangular também possui a menor área de superfície para um determinado volume se seus comprimentos de aresta forem iguais ao longo dos eixos cartesianos.
Para um cone sólido, as dimensões que minimizam a área de superfície também podem ser calculadas em forma fechada.
Agora você pode visualizar os sólidos mais eficientes para essas formas à medida que as dimensões gerais variam.
