Explore os espaços de função
Um espaço de função é um conjunto de funções de um determinado tipo, de um conjunto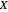 
a um conjunto 
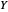. É chamado de espaço porque, em muitas aplicações, é um espaço topológico e é frequentemente associado a um espaço de medida.
Os espaços funcionais tendem a envolver conceitos topológicos muito gerais e abstratos. O domínio da entidade "FunctionSpace" codifica propriedades com mais de 125 espaços e as disponibiliza em um formato adequado para cálculos.
Por exemplo, os espaços de Lebesgue são definidos usando uma generalização natural da norma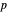 
para espaços vetoriais de dimensão finita. Um bom resumo das propriedades do espaço Lebesgue da ordem 
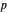sobre 
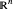pode ser obtido diretamente de uma consulta no Wolfram|Alpha, aqui customizada para exibir apenas os pods mais significativos.
Na verdade, existem muitas variedades de espaços de Lebesgue definidos, com base em seu domínio e espaço de medida.
Considere agora o caso especial do espaço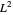 
, que tem a norma definida da seguinte forma.
Aqui, o contexto de PureMath é usado como um espaço reservado para objetos matemáticos que (ainda?) não foram incorporados à Wolfram Language.
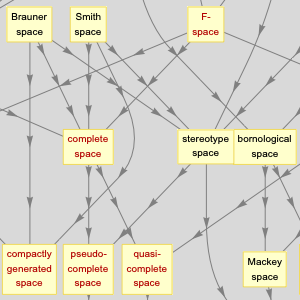
Informações sobre pessoas importantes que estudaram cada espaço também estão disponíveis.
Para facilitar, também é fornecida uma exibição tabular de várias notações em uso para cada espaço.
Como uma ilustração de como as informações neste domínio de entidade podem ser usadas, alguns cálculos simples são realizados.
Considere o espaço dual de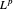 
(para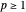 
).
Agora pegue o dual do espaço dual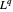 
e execute a simplificação simbólica na entidade parametrizada resultante.
Como isso é igual ao espaço original, você pode ver que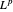 
é reflexivo, ex. 
.
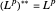Isso também pode ser calculado diretamente.
Informações mais detalhadas sobre espaços são fornecidas através da propriedade "TypesetDescription", que no caso de um espaço reflexivo fornece a seguinte definição rigorosa, juntamente com algumas descrições adicionais úteis.
