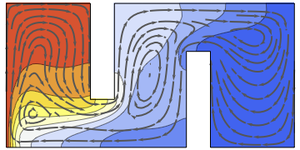
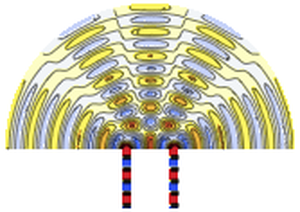
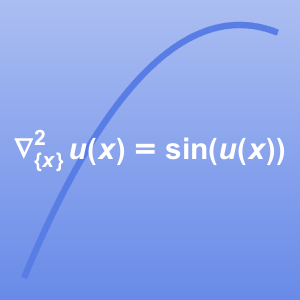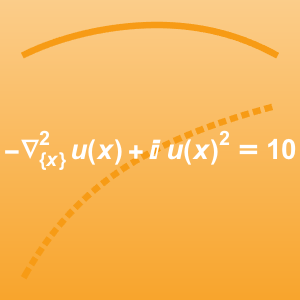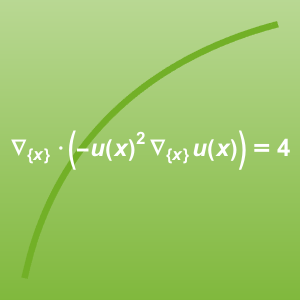アフィン共変ニュートン法
新しい求根アルゴリズムであるアフィン共変ニュートン法を使って，大きい方程式系の根を求める．
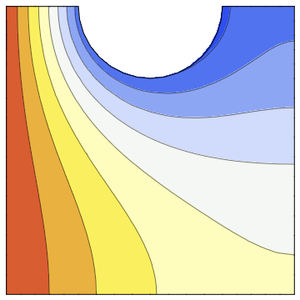
有限差分法を使って，非線形微分方程式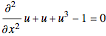
を離散化する．
離散化された方程式系のヤコビアンを設定する．
求根アルゴリズムの初期シードを設定する．
方程式系の根を求めるのに必要なステップ，評価，ヤコビアン評価の数を調べる．
その値を，新しく実装されたアフィン共変ニュートン法と比較する．
アフィン共変ニュートン法は根を求めるために必要なヤコビアン評価の回数を大きく減少させる．ヤコビアンの構築と評価は，大規模な方程式系では時間がかかるので，アフィン共変ニュートン法を使うことで根探索処理の時間が節約できる．
アフィン共変ニュートン法についての詳細は，ドキュメントに記載されている．
