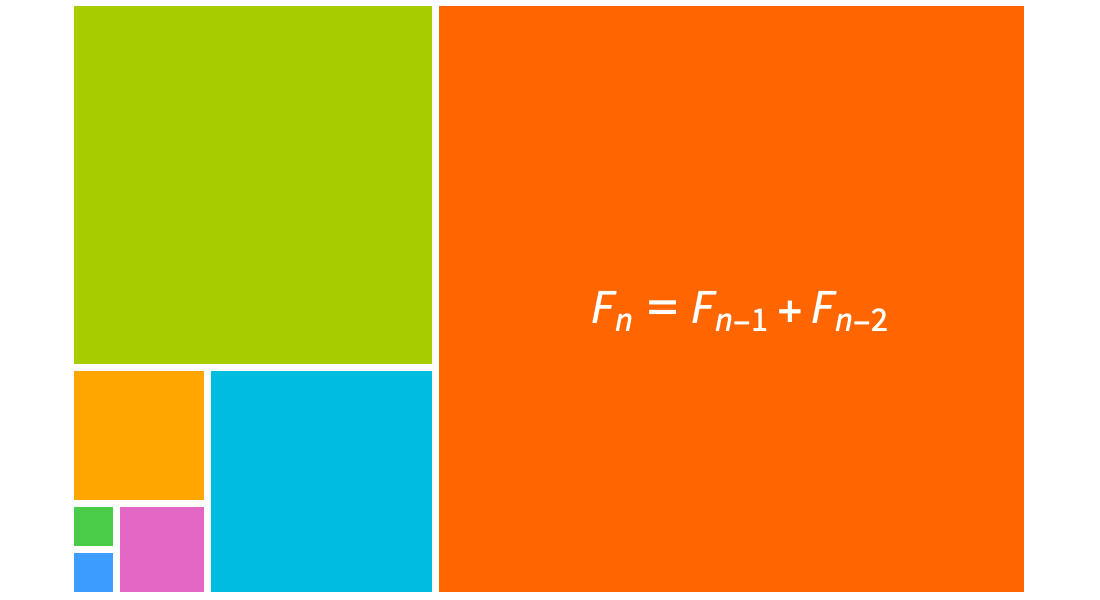WolframMathematical FunctionsA CORE PART OF
WOLFRAM LANGUAGE
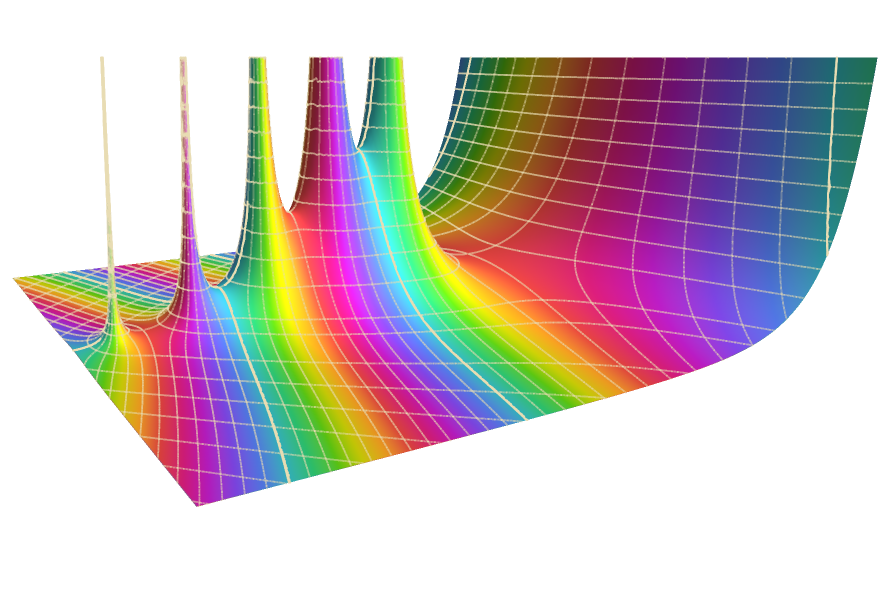
Define, compute and visualize.
Symbolic and numerical evaluation, visualization and asymptotic expansions of a large collection of mathematical functions—extensively documented and tightly integrated with all areas of Wolfram Language.
Most Complete Collection
With hundreds of elementary to advanced special functions, the broad collection is tightly integrated into symbolic and numerical solvers. Compute numerical results to any desired precision and find or simplify formulas. Extensive, multilevel and interactive documentation allows anyone to unleash their power.

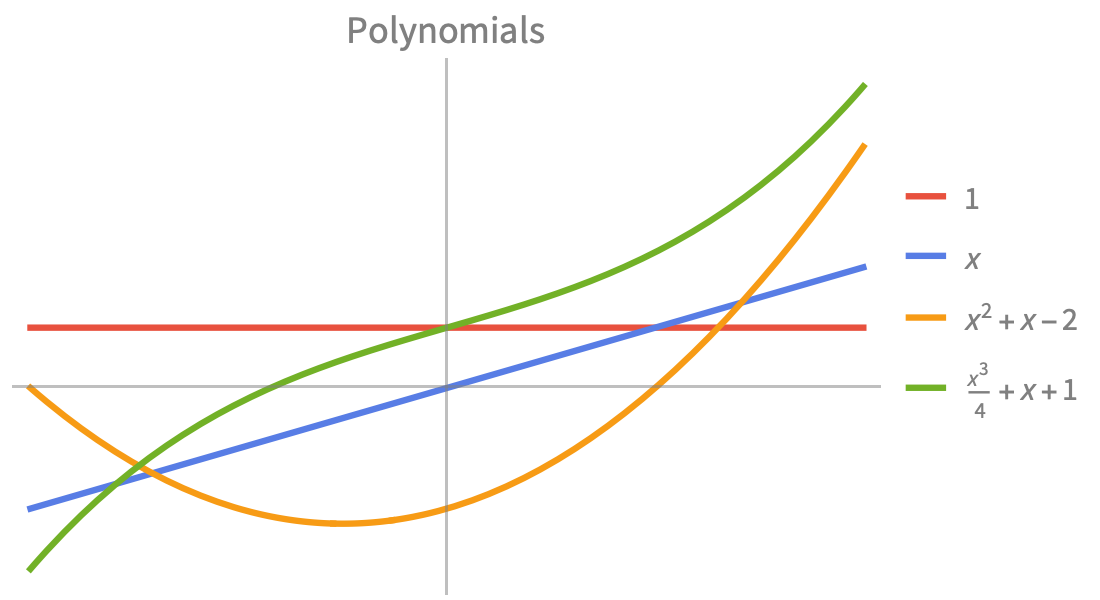
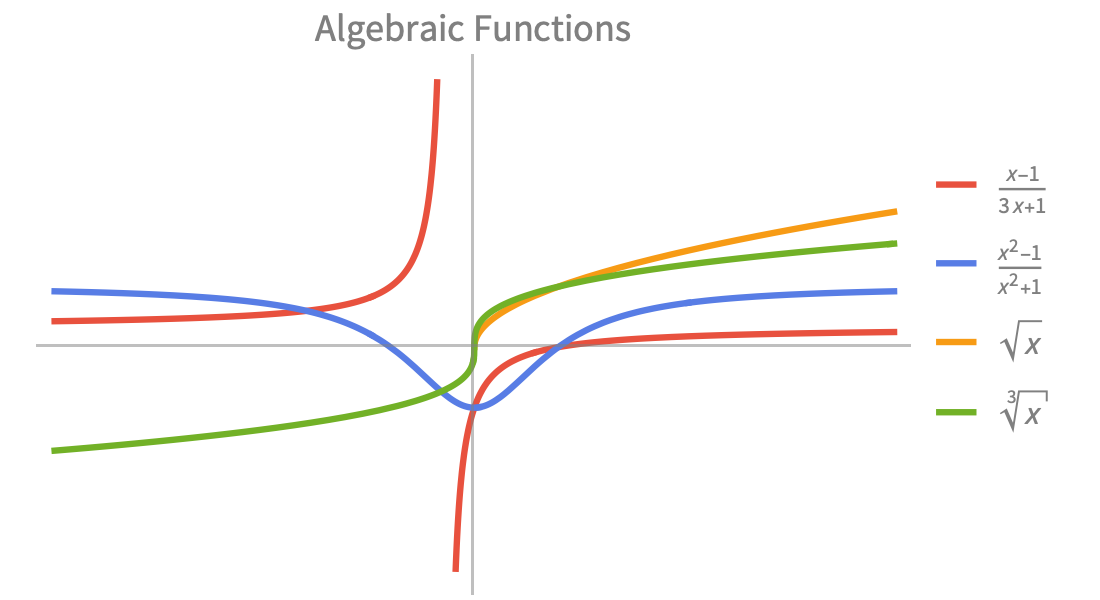
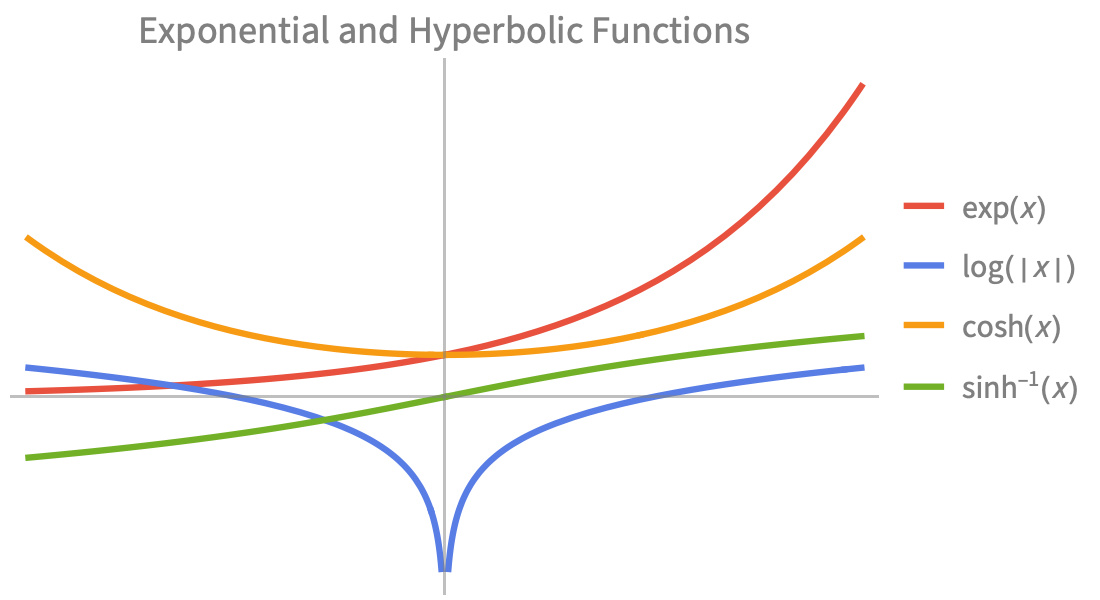
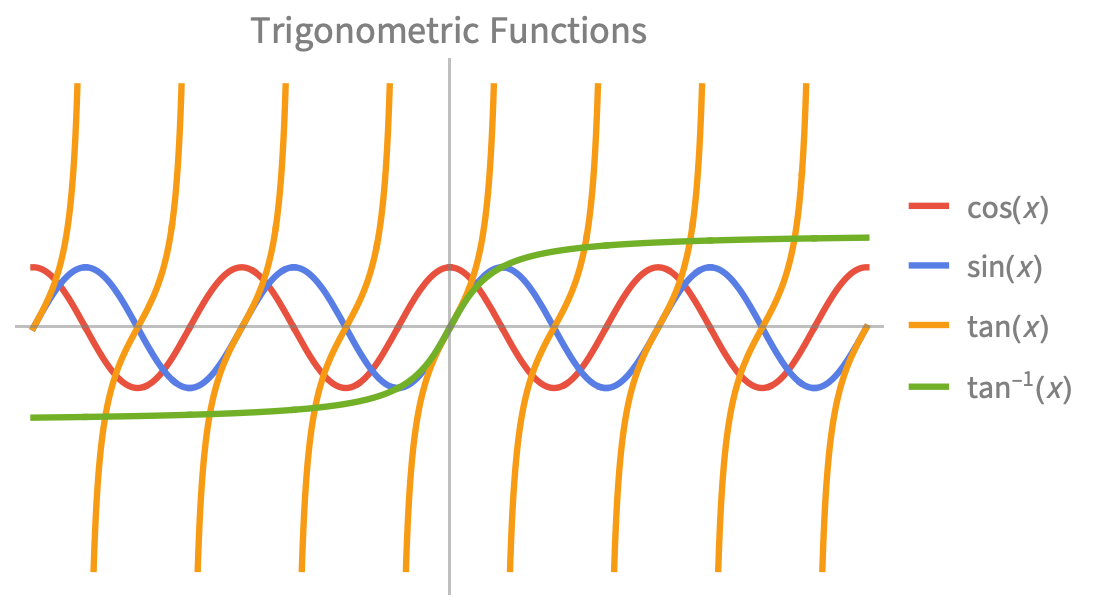
Elementary Functions
Fast, precise numeric and symbolic computation for science and engineering applications. Built-in exponential, trigonometric and hyperbolic functions to model combinations of growth, decay and oscillatory behavior.
Special Functions
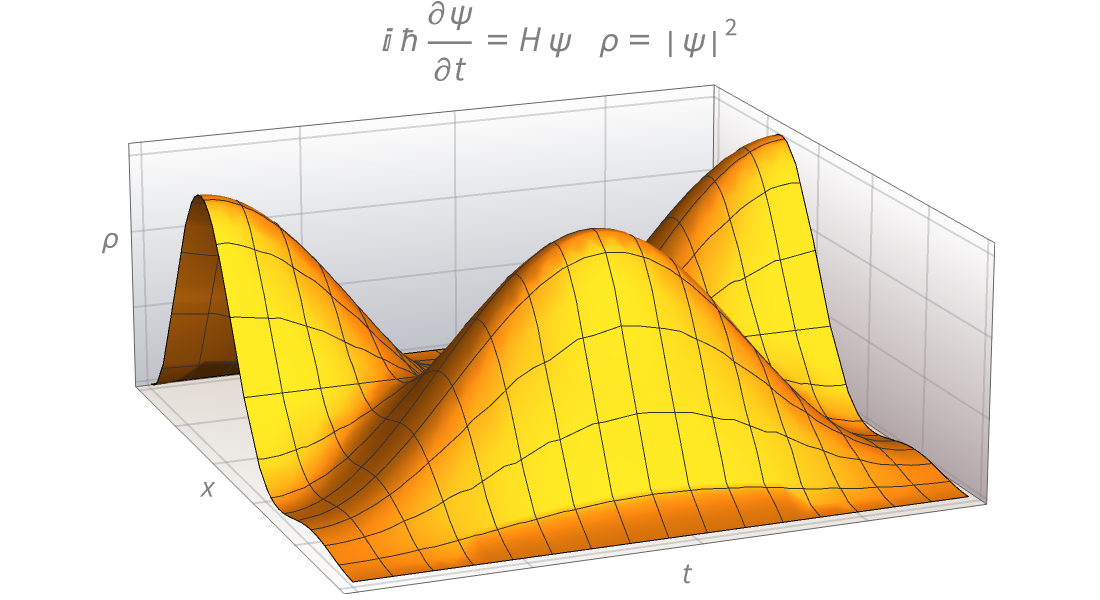
Solve problems in physics, engineering, probability and statistics with high‐precision numerics or symbolic series expansion.
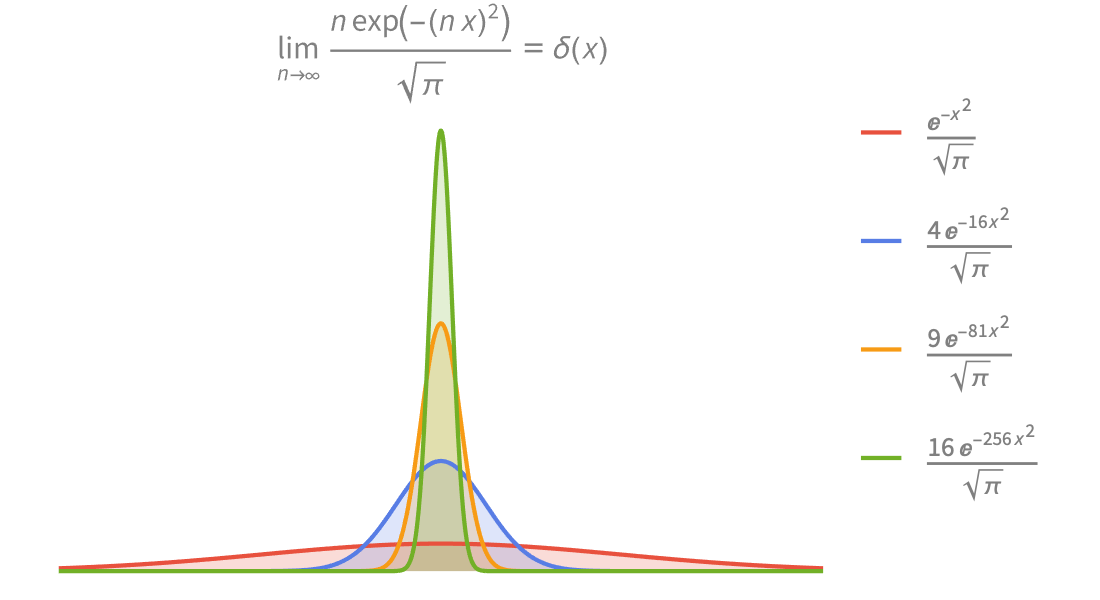
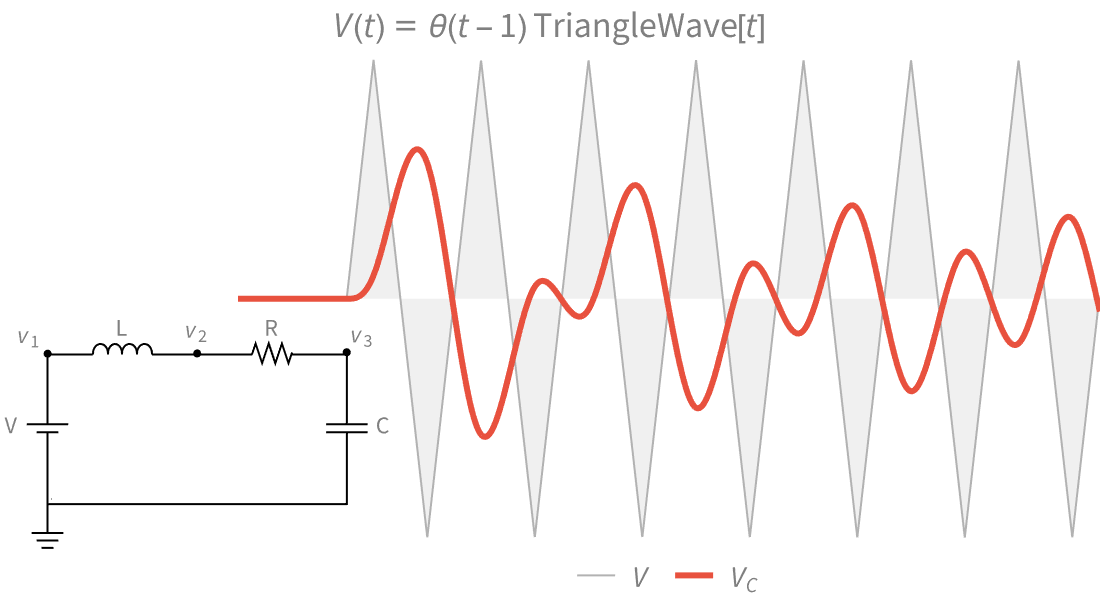
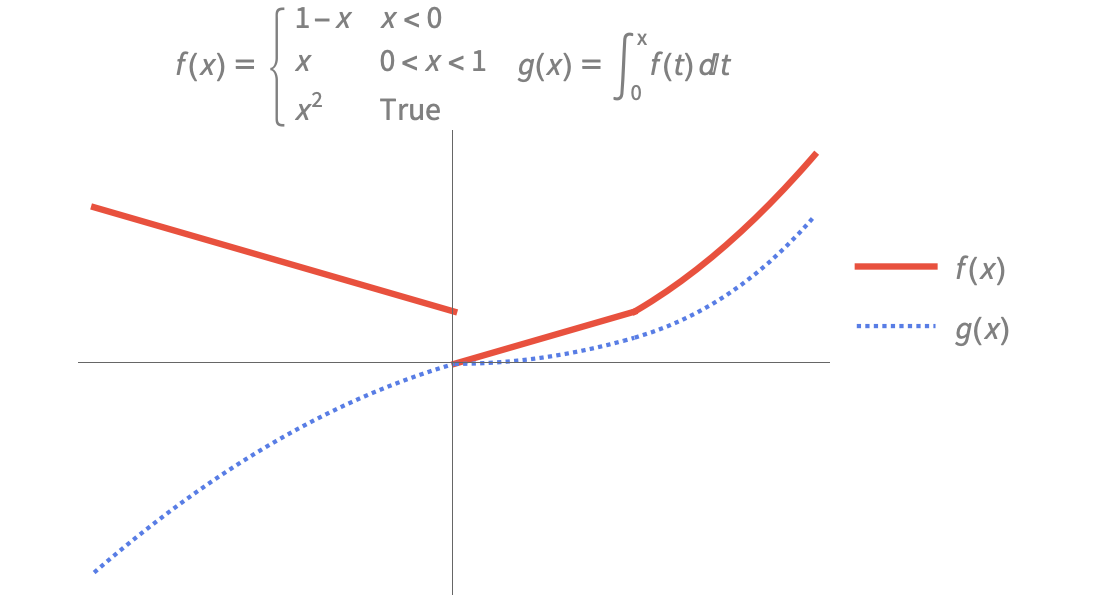
Piecewise and Generalized Functions
Model engineering and physical systems with a full range of pointwise-defined piecewise functions and generalized functions. Construct your own functions using Piecewise.
Integer Functions
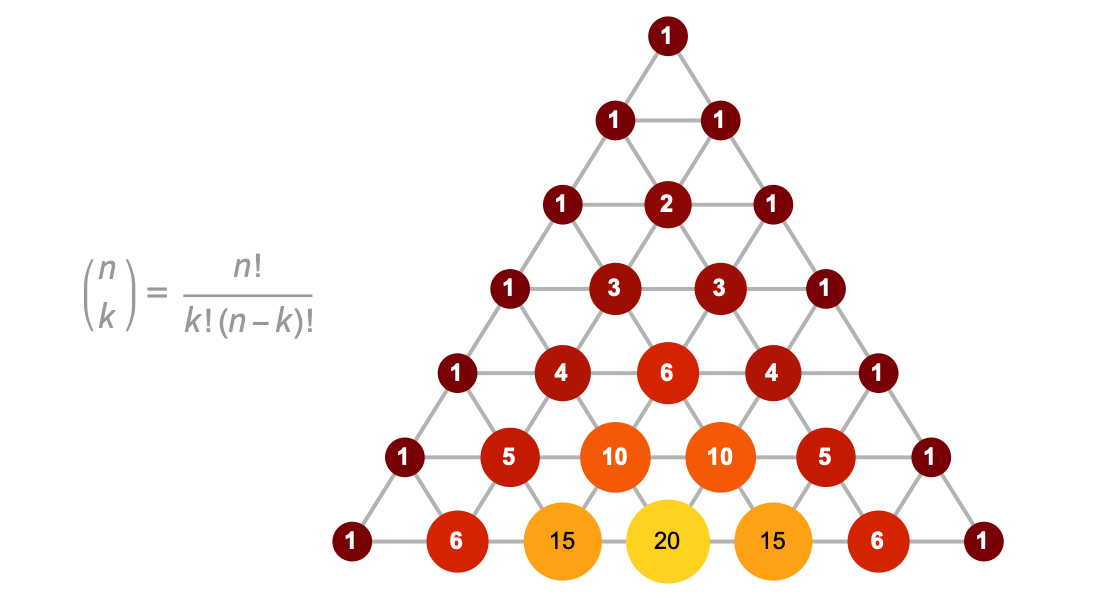
Explore sequences and series with binomial coefficients, Fibonacci and harmonic numbers and other integer functions. Use built-in symbolic summation, recurrence equation solving and sequence recognition to solve problems in combinatorics, the theory of algorithms and other domains.
Function Properties
Quickly compute more than 15 key mathematical properties of functions and their sums, products and compositions to ensure the mathematical validity of many procedures.

Symbolic Computation
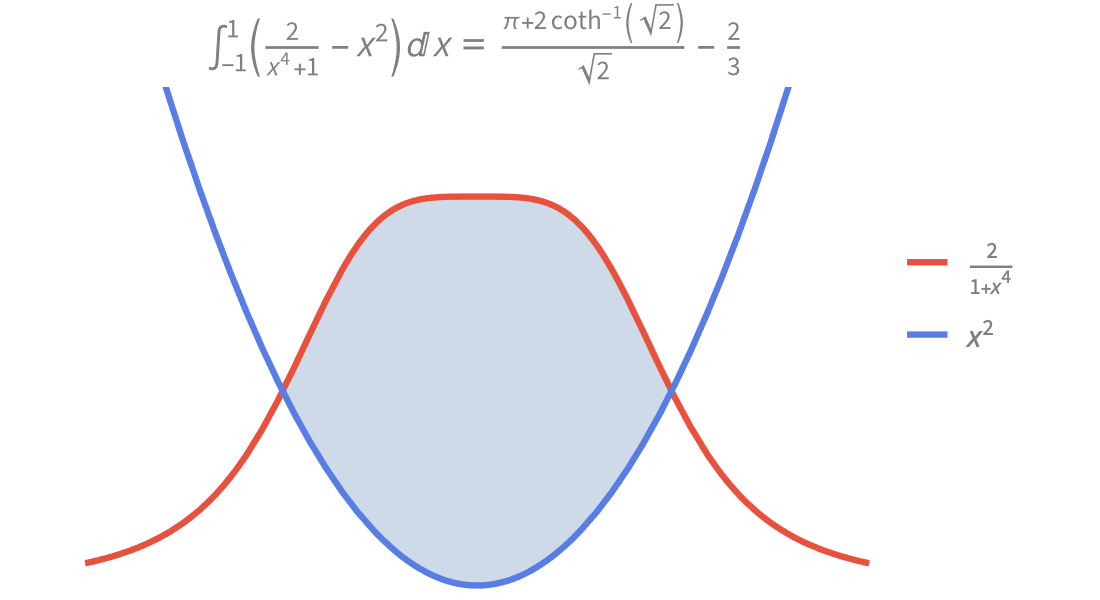
Get best-in-class, closed-form solutions to integrals, differential equations and dozens of other problems. Simplify formulas and compute exact answers. Input problems to symbolic solvers precisely and concisely, using the comprehensive set of mathematical functions.
Numerical Computation
Calculate the value of any mathematical function at machine precision or to a specified arbitrary precision. Compute with rigorous bounds using intervals, both on the real line and in the complex plane. Easily propagate statistical uncertainties. Input problems to numerical solvers accurately with any desired function.
Asymptotic Computation
Compute asymptotic approximations of functions for symbolic analysis of problems when exact symbolic evaluation fails and numerical evaluation is not reliable. A robust system for series allows any analytic function to be used in input, and generalized series can express results compactly by continuing to use needed mathematical functions.
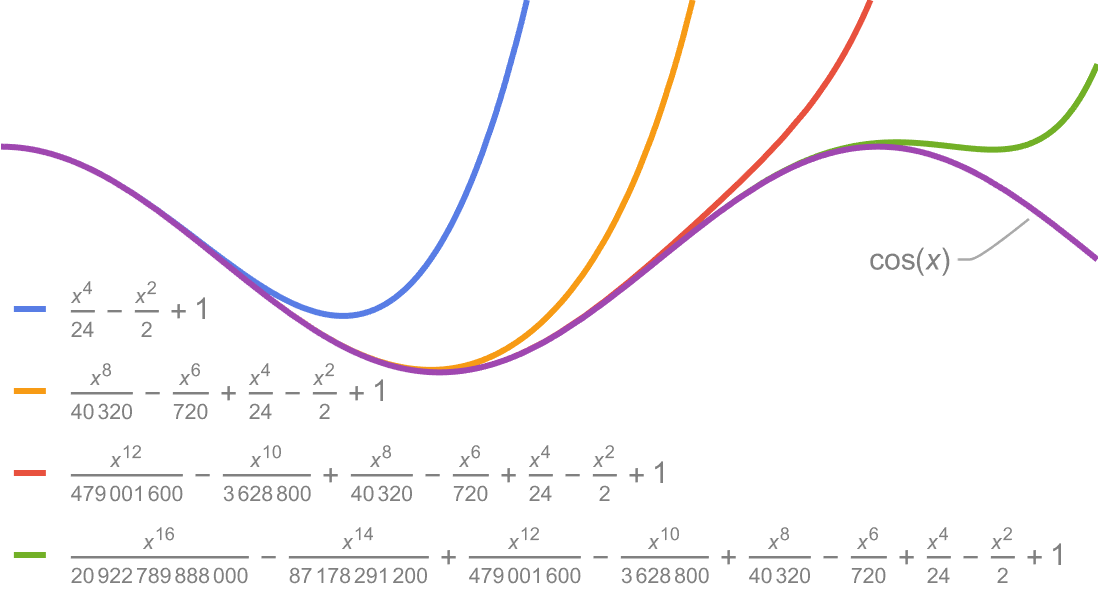
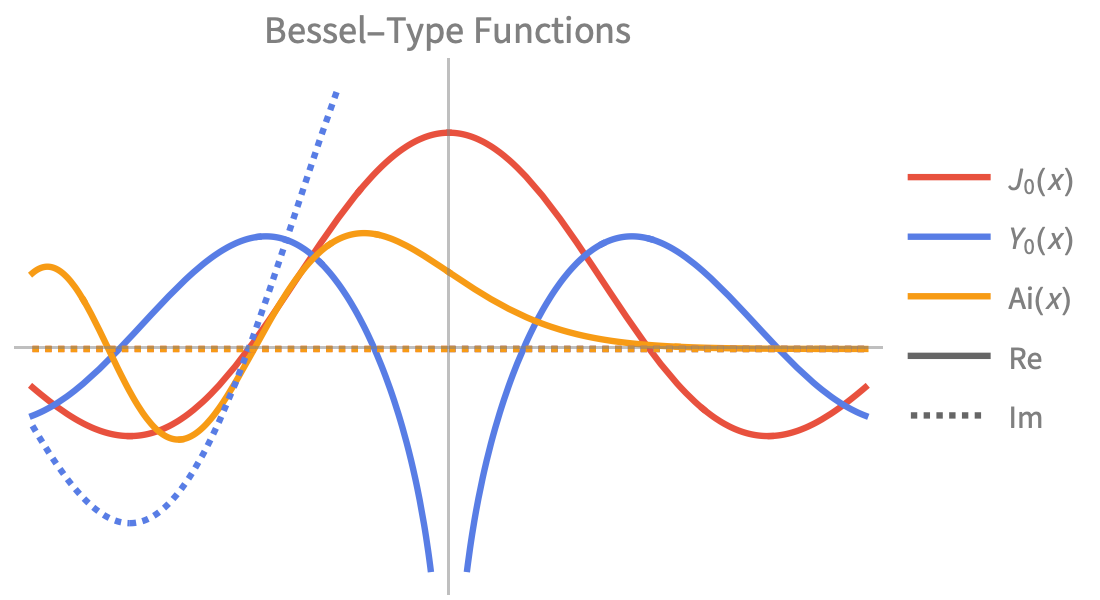
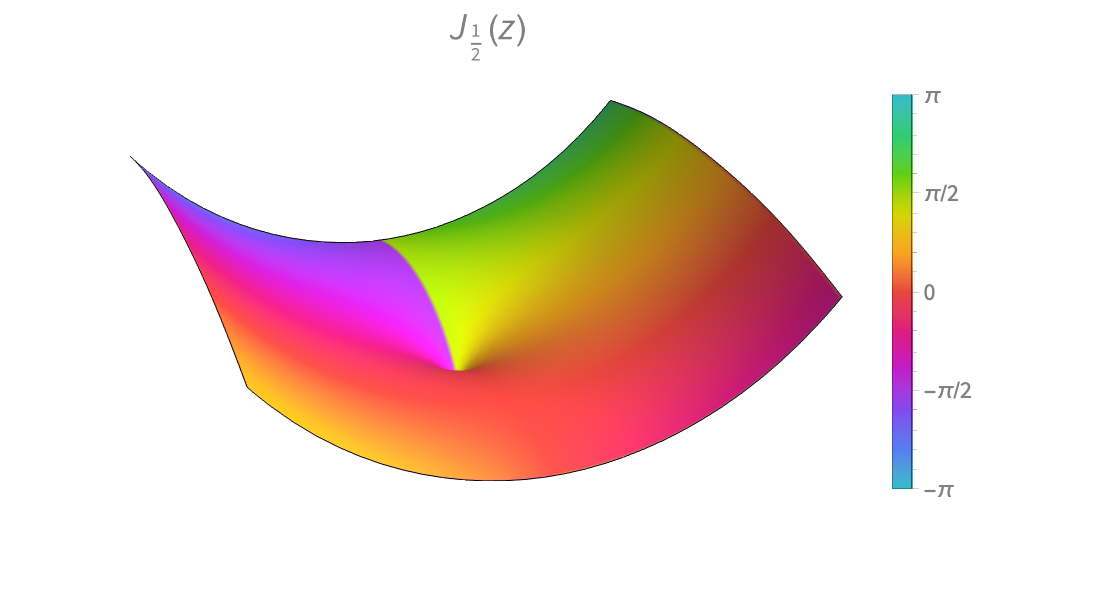
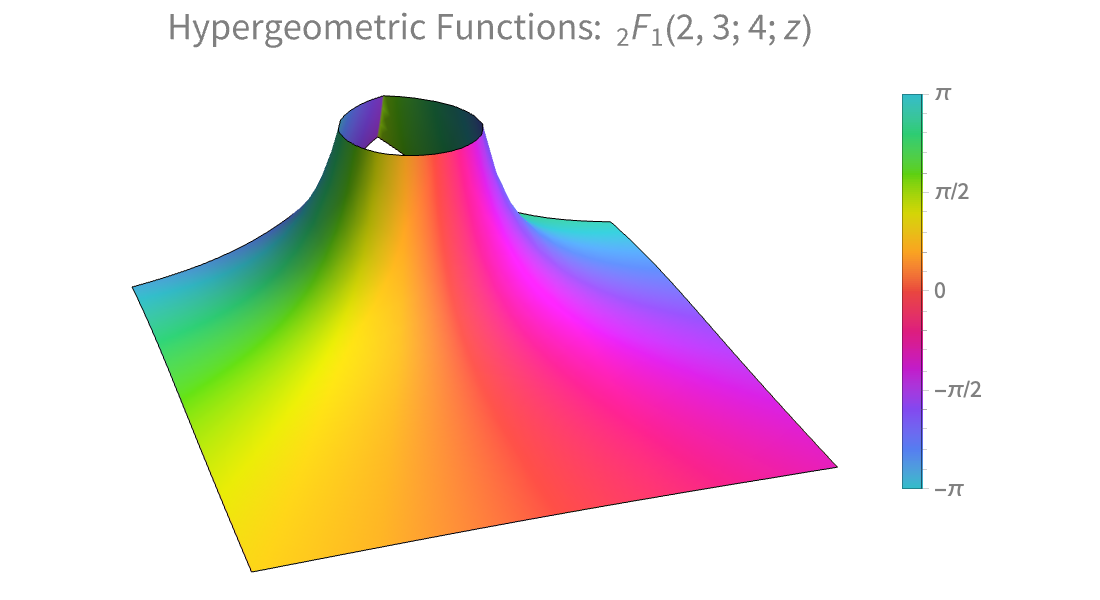
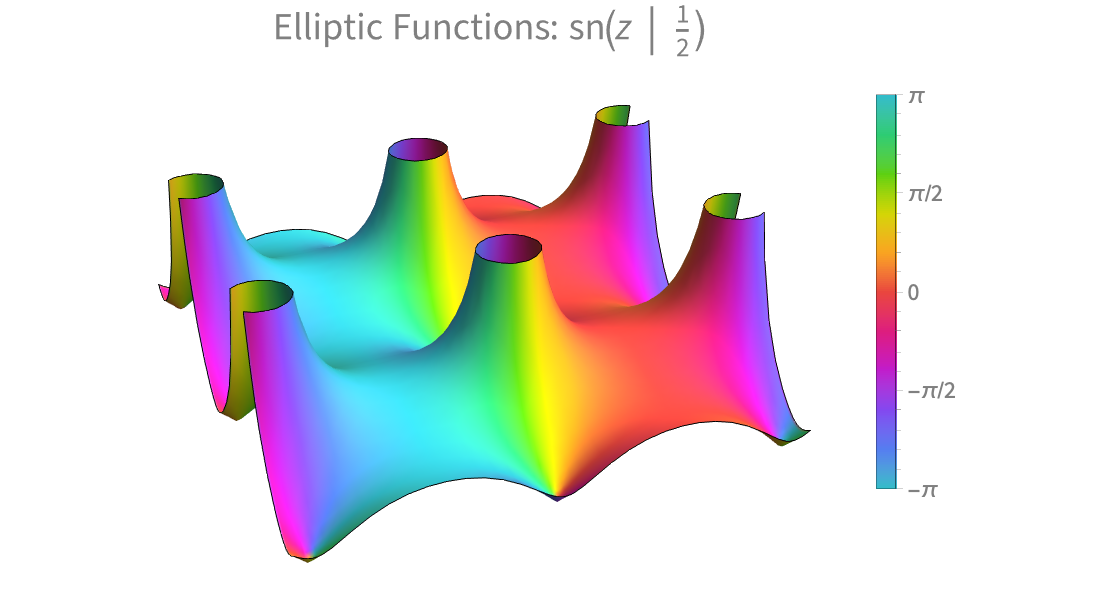
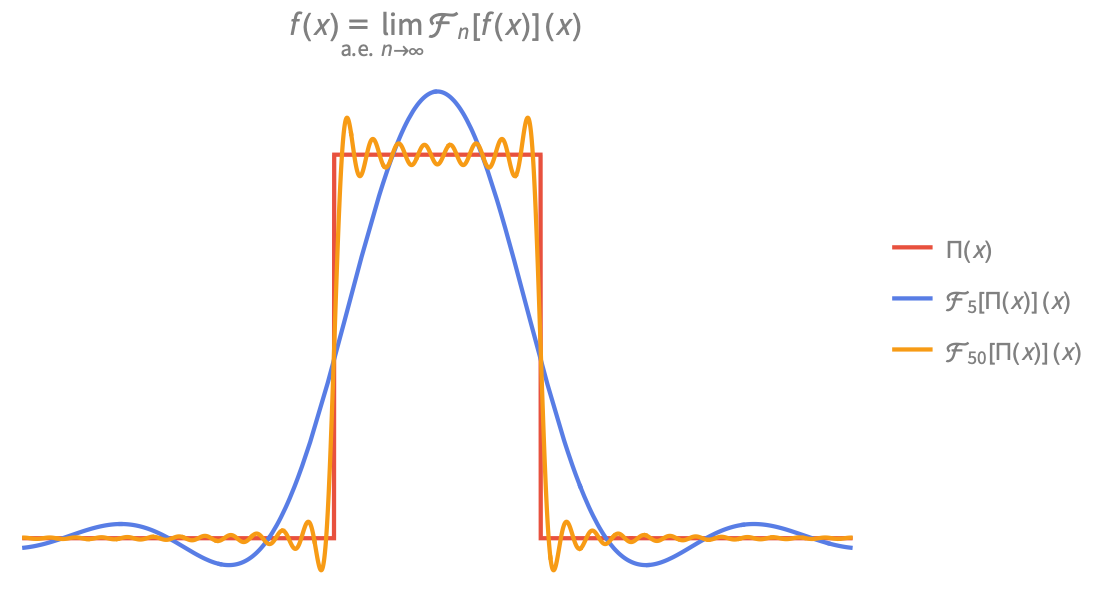
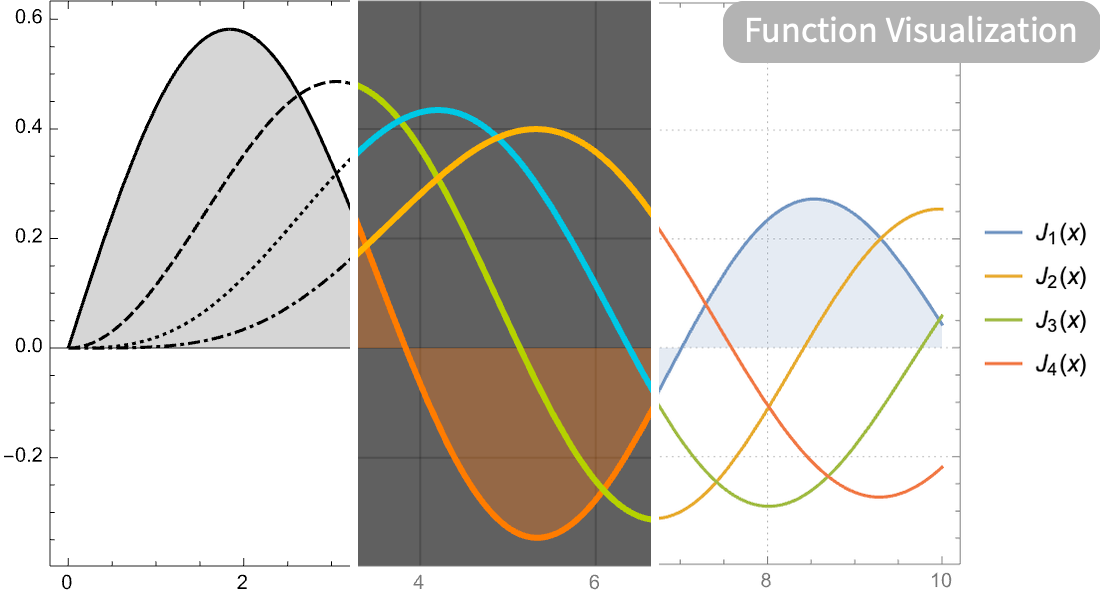
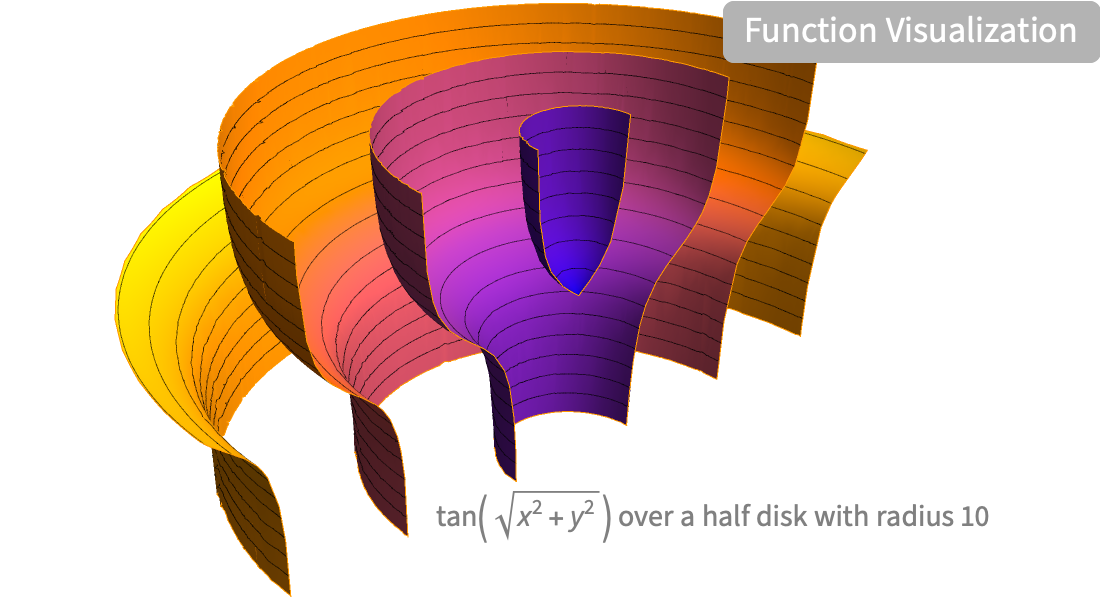
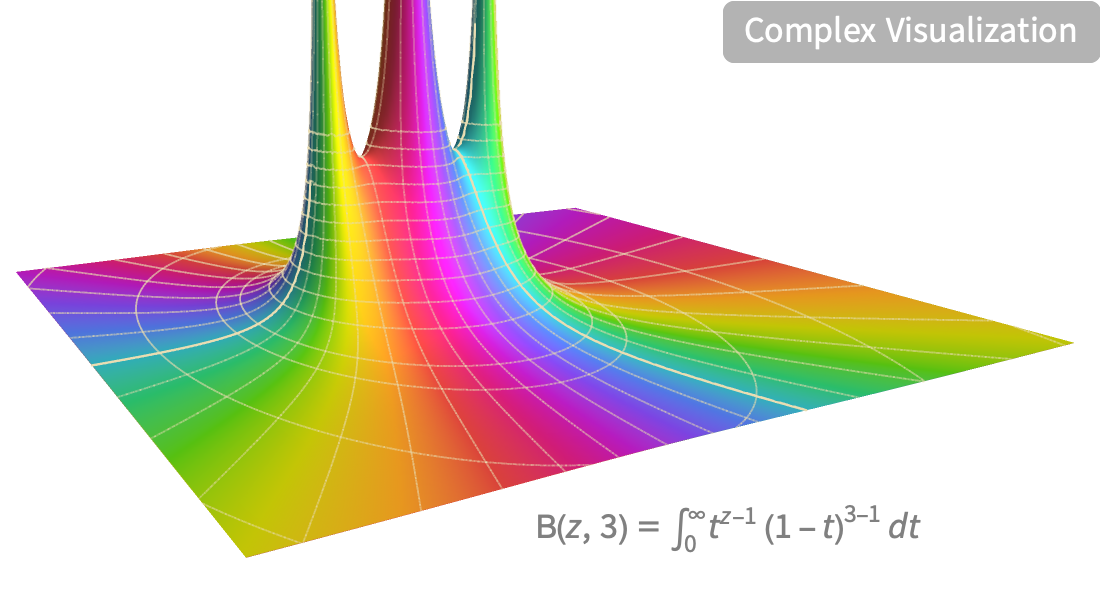
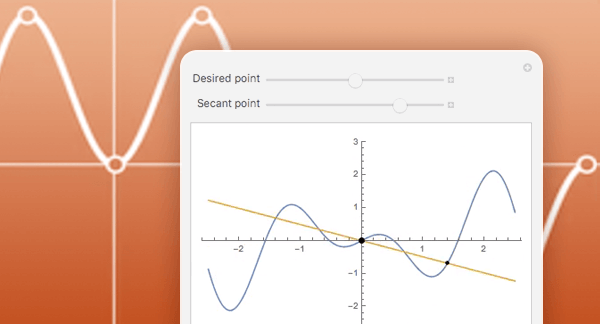
Visualization
Produce high-quality illustrations for reports and papers and gain insight into the behavior of mathematical functions.
Wolfram Mathematical Functions Documentation
Wolfram Mathematical Functions is an integrated part of Wolfram Language. The full system contains over 6,000 built-in functions covering all areas of computation—all carefully integrated so they work perfectly together.
 Wolfram Language
Wolfram LanguageFull Scope & Documentation
 Guide
Guide Guide
Guide Guide
Guide