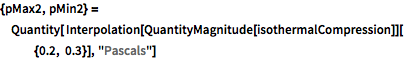Analyze the Stirling Cycle with Real-World Materials
Examine the Stirling cycle for 10 moles of air.
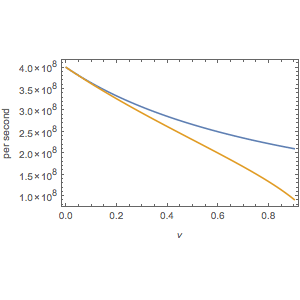
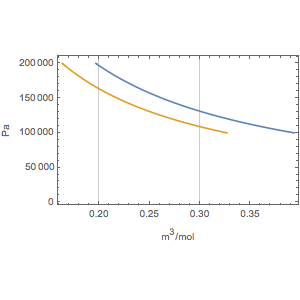
| Out[1]= |  |
Calculate the isothermal expansion and compression curves at 200 °C and 100 °C, respectively.
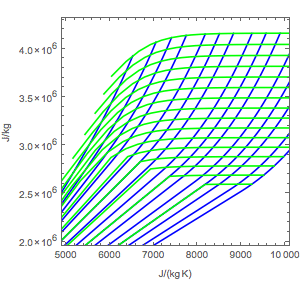
Create the 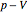 diagram.
diagram.
| Out[4]= | 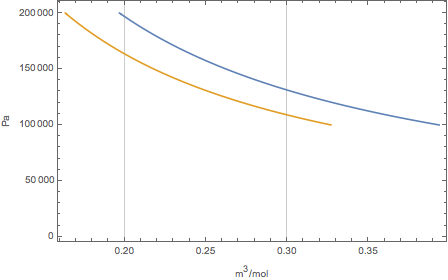 |
Calculate mechanical work through 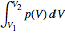 .
.
| Out[5]= | 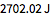 |
Find maximal and minimal pressures for expansion and compression.
| Out[6]= | 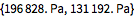 |
| Out[7]= | 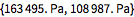 |
Calculate the change in internal energy.
| Out[8]= | 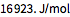 |
| Out[8]= | 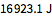 |
Using work and the change in internal energy, calculate efficiency.
| Out[9]= | 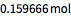 |
Compare with maximal possible Carnot efficiency.
| Out[10]= | 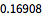 |


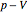 diagram.
diagram.

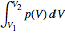 .
.