Mathematica 10 的新功能 › 增强的随机处理 ›

从数据估计隐马尔可夫过程 

从给定数据估计有三个可能输出的两状态隐马尔可夫过程.

In[1]:=
Click for copyable input
X
In[2]:=
Click for copyable input
X
Out[2]=

根据估计过程，计算数据的对数似然值.

In[3]:=
Click for copyable input
X
Out[3]=

估计连续输出的两状态过程.

In[4]:=
Click for copyable input
X

每个路径的叠加柱状图显示为高斯输出.

In[5]:=
Click for copyable input
X
Out[5]=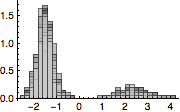

比较默认的 Baum–Welch 方法和维特比训练产生的结果.

In[6]:=
Click for copyable input
X
Out[6]=
In[7]:=
Click for copyable input
X
Out[7]=

Baum–Welch 估计过程中数据有更高的对数似然值.

In[8]:=
Click for copyable input
X
Out[8]=

Related Examples

Hidden Markov Processes with Discrete or Continuous, Univariate or Multivariate Emissions » Hidden Markov Processes with Silent States » Find Hidden States Underlying Given Emissions of HMM Process » Estimate Hidden Markov Processes from Data »
Perform Typo Correction without a Dictionary » Track Player Movement in a First-Person Shooter Game » Find a Splice Site in a DNA Sequence » Track Lizard Movement with a Capture-Recapture Model »
Use TransformedProcess to Create a Custom Process » Study the Stochastic Exponential Function » Simulate the Surplus Process for Insurance » Model Option Prices Using Merton Jump-Diffusion  »
Generate White Noise Based on Any Distribution » Apply ARMA Filter to a Heavy-Tailed White Noise Process » Test for Serial Correlation » Fractional Gaussian Noise versus FARIMA Noise »
Improved Support of Random Processes in Expectation » Improved Support of Random Processes in Probability » Identify Regularly Sampled Ornstein–Uhlenbeck Process as an Autoregressive Process » Improved Documentation for Probability and Statistics »
de en es ja pt-br