無音状態を持つ隠れマルコフ過程
無音状態を持つ隠れマルコフ過程は，隠れ状態力学の剛性位相（遷移行列は疎行列ということ）で使われることが多い．これは，選ばれたトポロジーのもとではあり得ない観測値状態間の遷移を可能にする．構造化された遷移行列のおかげで，無音状態を持つ隠れマルコフモデルは，密なものよりも推定が簡単なことがよくある．
6つの観察不可能な状態のうちの一つである系の初期尤度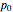 
と，これらの状態間の条件付き遷移確率の行列 
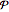を定義する．
| In[1]:= |  X |
隠れ状態間の遷移のトポロジーを可視化する．
| In[2]:= |  X |
| Out[2]= |  |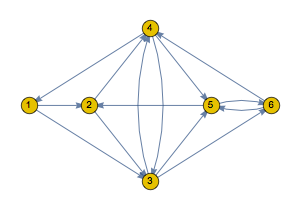
可観測なすべての状態に対して分類信号を発する系の周波数を定義する．観測値には1から6のラベルが付けられる．系が状態3または4，つまり無音状態にある場合は，観測値は起こらない．
| In[3]:= | 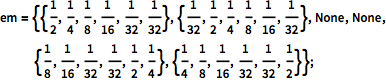 X |
観察可能な観測値を記述する隠れマルコフ過程を定義する．
| In[4]:= |  X |
観測値列のシミュレーション．
| In[5]:= |  X |
| Out[5]= |  |
系に内在する観察不可能状態で最も可能性の高い列を見付ける．
| In[6]:= |  X |
| Out[6]= |  |
状態のデコードされた列は，無音状態があるため観測値列よりも長い．デコードされた隠れ状態の列を可視化する．
| In[7]:= |  X |
 |
すべての観測値列に同じ確率を割り当てる，隠れ状態のない隠れマルコフ過程を見付ける．
| In[8]:= |  X |
| Out[8]= |  |
観測値の短い列を構築し，両方の過程がそれらに同じ尤度を割り当てることを確認する．
| In[9]:= |  X |
| In[10]:= |  X |
| In[11]:= |  X |
| In[12]:= |  X |
| Out[12]= |  |
より長い観測値列の集合体を生成し，それを使って無音状態を持つ隠れマルコフ過程のパラメータを推定する．
| In[13]:= |  X |
| In[14]:= |  X |
| Out[14]= |  |
観測値の対数尤度を比較する．
| In[15]:= |  X |
| Out[15]= |  |
| In[16]:= |  X |
| Out[16]= |  |
