有沉默状态的隐马尔可夫过程
有沉默状态的隐马尔可夫过程通常用于隐藏状态动态的刚性严格拓扑，例如稀疏的转移矩阵，使的在所选拓扑中的输出状态间启动转换是不可能的. 由于转移矩阵的结构，有沉默状态的隐马尔可夫模型通常比其更密集的类拟物更容易估计.
定义系统初始似然函数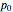 
为6个可能的非可观测状态之一，以及这些状态间条件转移概率矩阵 
.
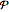| In[1]:= |  X |
可视化在隐藏状态间转换的拓扑.
| In[2]:= |  X |
| Out[2]= |  |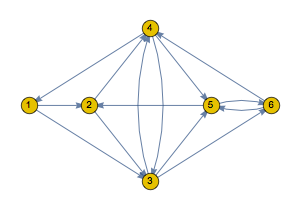
对每个非可观测状态，定义系统发出的一个分类信号的频率. 以1到6标签标注输出. 当系统发现其在状态3或4，即这些为沉默状态时，没有给出输出.
| In[3]:= | 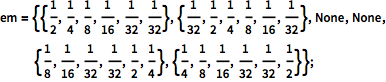 X |
定义描述可观察输出的隐马尔可夫过程.
| In[4]:= |  X |
模拟一个输出序列.
| In[5]:= |  X |
| Out[5]= |  |
找到系统根本的不可观察状态的最可能序列.
| In[6]:= |  X |
| Out[6]= |  |
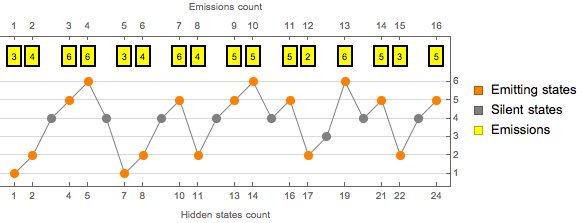
由于沉默状态的存在，注意到状态的解码序列长于输出（emissions）序列. 可视化解码的隐藏状态序列.
| In[7]:= |  X |
 |
找出没有隐藏状态，对所有输出（emissions）序列赋值相同概率的隐马尔可夫过程.
| In[8]:= |  X |
| Out[8]= |  |
构建短的输出（emissions）序列，并确认两个过程都赋值其相同似然度.
| In[9]:= |  X |
| In[10]:= |  X |
| In[11]:= |  X |
| In[12]:= |  X |
| Out[12]= |  |
生成一个更长的输出（emissions）序列的集合，并用其估计沉默状态的隐马尔可夫过程的参数.
| In[13]:= |  X |
| In[14]:= |  X |
| Out[14]= |  |
比较输出（emissions）的对数似然值.
| In[15]:= |  X |
| Out[15]= |  |
| In[16]:= |  X |
| Out[16]= |  |
