Procesos ocultos de Markov con estados silenciosos
Los procesos ocultos de Markov con estados silenciosos son usualmente utilizados con tipología rígida de dinámicas de estados ocultos; es decir, la matriz de transición es escasa para permitir transiciones entre estados emisores que son imposibles bajo la topología elegida. Gracias a la matriz de transición estructurada, los modelos ocultos de Markov con estados silenciosos son con frecuencia más fáciles de estimar que sus análogos densos.
Defina las probabilidades iniciales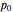 
del proceso que está en uno de los seis posibles estados no observables, así como la matriz 
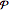de las probabilidades condicionales de transición entre estos estados.
| In[1]:= |  X |
Visualice la topología de transiciones entre estados ocultos.
| In[2]:= |  X |
| Out[2]= |  |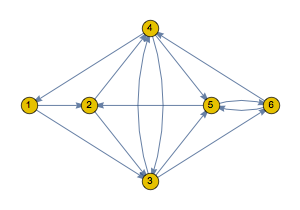
Defina frecuencias del sistema que emite una señal categórica para cada estado no observable. Las emisiones son etiquetadas del 1 al 6. No se realizan emisiones cuando el sistema se encuentra en el estado 3 o 4; en otras palabras, estos estados son silenciosos.
| In[3]:= | 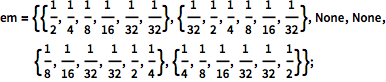 X |
Defina un proceso oculto de Markov que describe emisiones observables.
| In[4]:= |  X |
Simule una secuencia de emisiones.
| In[5]:= |  X |
| Out[5]= |  |
Encuentre la secuencia más probable de los estados no observables subyacentes del sistema.
| In[6]:= |  X |
| Out[6]= |  |
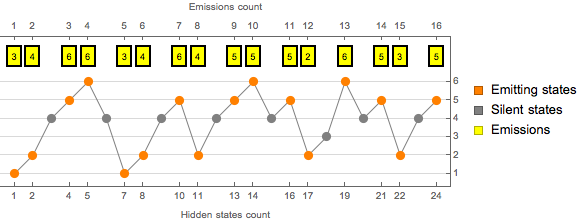
Note que la secuencia decodificada de estados es más larga que la secuencia de las emisiones, debido a la presencia de los estados silenciosos. Visualice la secuencia de estados ocultos decodificados.
| In[7]:= |  X |
 |
Encuentre el procesos oculto de Markov sin estados ocultos que asignan las mismas probabilidades para todas las secuencias de emisión.
| In[8]:= |  X |
| Out[8]= |  |
Construya secuencias cortas de emisiones y confirme que ambos procesos les asignan probabilidades iguales.
| In[9]:= |  X |
| In[10]:= |  X |
| In[11]:= |  X |
| In[12]:= |  X |
| Out[12]= |  |
Genere un conjunto de secuencias de emisiones más largas y utilícelo para estimar los parámetros del proceso oculto de Markov con estados silenciosos.
| In[13]:= |  X |
| In[14]:= |  X |
| Out[14]= |  |
Compare probabilidades de sesión de emisiones.
| In[15]:= |  X |
| Out[15]= |  |
| In[16]:= |  X |
| Out[16]= |  |
