規則的にサンプルされたオルンシュタイン・ウーレンベック過程を自己回帰過程として同定する
Mathematica 10では過程のスライスの計算のサポートが向上しているため,多変量過程のスライスにモーメント法をそのまま使って2つの過程間で等価法則が設定できる.
自己回帰(AR)過程とオルンシュタイン・ウーレンベック(OU)過程はともにガウス過程であり,平均および分散の関数により判定される.
| In[1]:= | X |
スライス分布にモーメント法を使い,等間隔時間格子で定常AR過程のパラメータを定常OU過程の制約にマッチさせる.
| In[2]:= | X |
| In[3]:= | 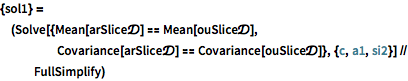 X |
| Out[3]= |
共分散関数が記号的遅れに一致していることを確認する.
| In[4]:= | X |
| Out[4]= |
| In[5]:= | X |
| Out[5]= |
初期条件付きのAR過程とOU過程の練習を繰り返す.
| In[6]:= | X |
| In[7]:= | X |
| In[8]:= | 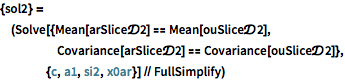 X |
| Out[8]= |
自己回帰表現を使って,等間隔時間格子上でオルンシュタイン・ウーレンベックをサンプルする.
| In[9]:= | X |
| Out[9]= | 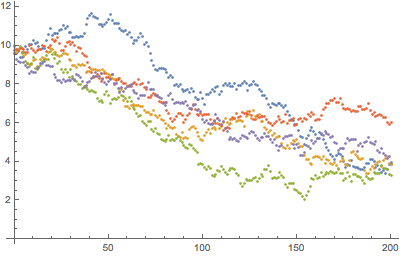 |
























