Identifique processo Ornstein–Uhlenbeck regularmente amostrado como um processo autorregressivo
O suporte aprimorado do Mathematica 10 para computação com fatias de processo permite que você use diretamente método de momentos para fatias de processo multivariado para estabelecer a equivalência de lei entre os dois processos.
Tanto o processo autorregressivo (AR) quanto o processo Ornstein–Uhlenbeck (OU) são processos Gaussianos, determinados por suas funções de média e covariância.
| In[1]:= | X |
Use o método de momentos para distribuições de fatias para combinar os parâmetros do processo AR estacionário às restrições do processo OU estacionário a uma grade de tempo regular.
| In[2]:= | X |
| In[3]:= | 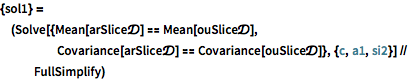 X |
| Out[3]= |
Confirme que as funções de covariância concordam com atraso simbólico.
| In[4]:= | X |
| Out[4]= |
| In[5]:= | X |
| Out[5]= |
Repita o exercício para processos AR e OU com condições iniciais.
| In[6]:= | X |
| In[7]:= | X |
| In[8]:= | 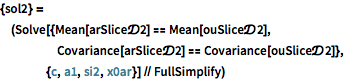 X |
| Out[8]= |
Use representação autorregressiva para amostrar o processo Ornstein–Uhlenbeck em uma grade de tempo regular.
| In[9]:= | X |
| Out[9]= | 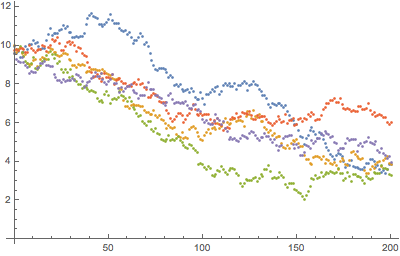 |
























