Einen regelmäßige Ornstein–Uhlenbeck-Prozess als autoregressiven Prozess identifizieren
Die verbesserte Unterstützung für Berechnungen mit Prozessabschnitten in Mathematica 10 ermöglicht es Ihnen, die Momentenmethode für multivariate Prozessabschnitte anzuwenden, um die Äquivalenz zwischen zwei Prozessen herzustellen.
Sowohl autoregressive (AR) Prozesse als auch Ornstein–Uhlenbeck (OU)-Prozesse sind Gaußsche Prozesse, die über ihre Mittelwertfunktion und Kovarianzfunktion bestimmt werden.
| In[1]:= | X |
Wenden Sie die Momentenmethode auf die Abschnittsverteilung an, um die Parameter des stationären AR-Prozesses an den stationären OU-Prozess, der ein regelmäßiges Zeitgitternetz benötigt, anzugleichen.
| In[2]:= | X |
| In[3]:= | 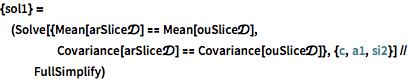 X |
| Out[3]= |
Vergewissern Sie sich, dass die Kovarianzfunktionen mit dem symbolischen Lag übereinstimmen.
| In[4]:= | X |
| Out[4]= |
| In[5]:= | X |
| Out[5]= |
Wiederholen Sie die Übung bei AR- und OU-Prozessen mit Anfangsbedingungen.
| In[6]:= | X |
| In[7]:= | X |
| In[8]:= | 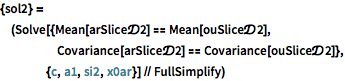 X |
| Out[8]= |
Verwenden Sie die autoregressive Darstellung, um einen Ornstein–Uhlenbeck-Prozess auf einem regelmäßigen Zeitgitter zu veranschaulichen.
| In[9]:= | X |
| Out[9]= | 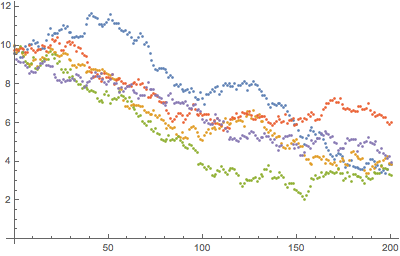 |
























