Vektorielle Modelle vs. univariate Komponentenmodelle
Ermitteln Sie die stündlichen Temperaturwerte für Champaign, Illinois im Mai 2014.
| In[1]:= | X |
| In[2]:= |  X |
Berechnen Sie mit TimeSeriesAggregate die täglichen Mindest- und Höchsttemperaturen.
| In[3]:= | X |
Kombinieren Sie diese zu einer vektoriellen Zeitreihe.
| In[4]:= |  X |
| Out[4]= |
| Out[5]= | 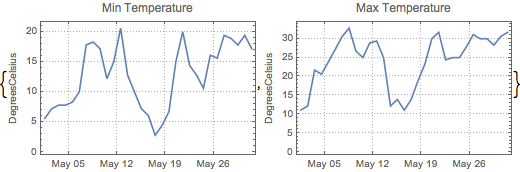 |
Der erste Teil der Daten wird zur Ermittlung eines Modells verwendet, während die restlichen Daten als Referenz für die Prognose dienen.
| In[6]:= | X |
Die Temperaturen sind kreuzkorreliert.
| In[7]:= | X |
| Out[7]= | 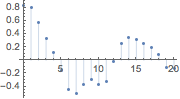 |
Stellen Sie die Daten in einem vektoriellen Modell dar.
| In[8]:= | X |
| Out[8]= |
Erstellen Sie eine Prognose für die nächsten 5 Tage.
| In[9]:= | X |
| Out[10]= | 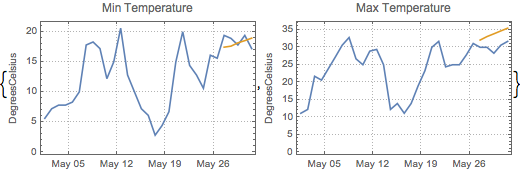 |
Finden Sie separate univariate Modelle desselben Typs für Höchst- und Mindesttemperaturen, jedoch für längere Folgen.
| In[11]:= |  X |
| Out[11]= |
| In[12]:= |  X |
| Out[12]= |
Kombinieren Sie die univariaten Prognosen, um sie graphisch darzustellen.
| In[13]:= |  X |
| Out[13]= |
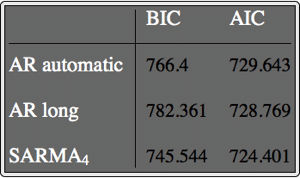
Vergleichen Sie die Prognosen.
| In[14]:= | X |
| Out[15]= | 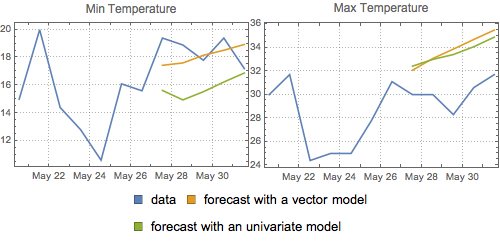 |
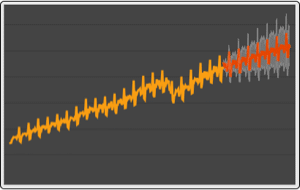
Stellen Sie die vektorielle Prognose und die 95 %-Konfidenzbänder graphisch dar.
| Out[17]= | 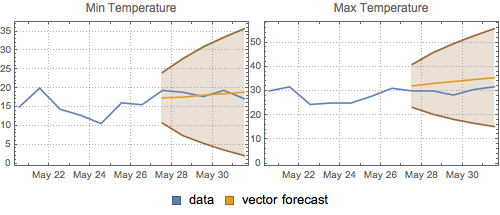 |
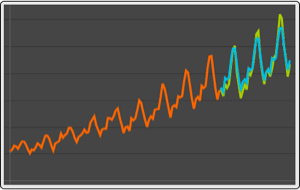
Stellen Sie die univariaten Prognosen und die 95 %-Konfidenzbänder graphisch dar.
| Out[20]= | 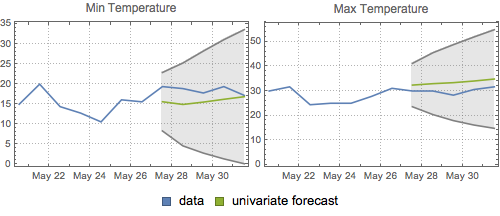 |
Vergleichen Sie beide Prognosen und die entsprechenden Konfidenzbänder.
| Out[21]= | 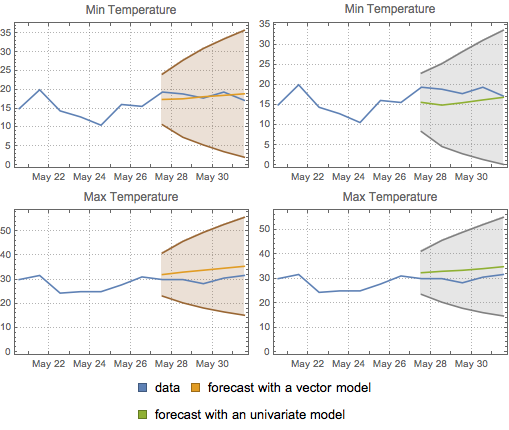 |