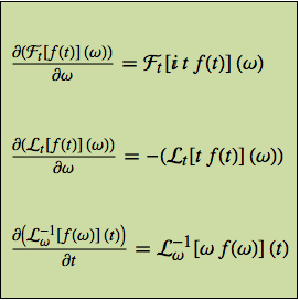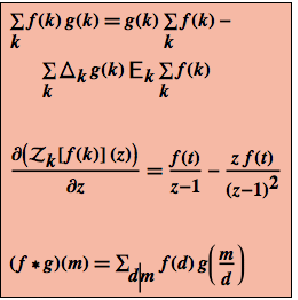Berechnungen mit Integraloperatoren
Die Eigenschaften von Integraloperatoren und anderer formaler Operatoren werden auf ihre inaktiven Formen angewendet.
Integraloperatoren sind z.B. die Funktionen LaplaceTransform, FourierTransform und Convolve.
| In[1]:= |  X |
Die Ableitungen dieser Operatoren nach dem letzten Argument können durch den Integraloperator selbst ausgedrückt werden.
| In[2]:= |  X |
| Out[2]= |  |
| In[3]:= |  X |
| Out[3]= |  |
| In[4]:= |  X |
| Out[4]= |  |
In all diesen Ableitungen ist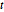 
eine Scheinvariable, daher sind die Ableitungen nach dieser Variablen Null.
| In[5]:= |  X |
| Out[5]= |  |
| In[6]:= |  X |
| Out[6]= |  |
| In[7]:= |  X |
| Out[7]= |  |
Da alle Operatoren linear sind, können Ableitungen von den Parametern unkompliziert durchgeführt werden.
| In[8]:= |  X |
| Out[8]= |  |
| In[9]:= |  X |
| Out[9]= |  |
| In[10]:= |  X |
| Out[10]= |  |
