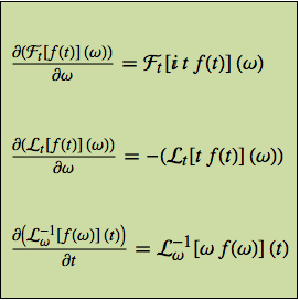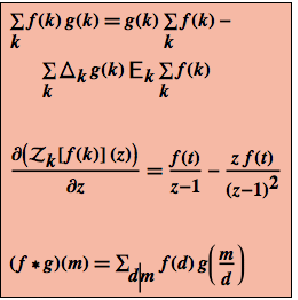Compute com transformadas integrais 

Propriedades de integrais e outros operadores formais são aplicadas a suas formas inativas.

Operadores integrais incluem LaplaceTransform, FourierTransform e Convolve.

In[1]:=

X lt = Inactive[LaplaceTransform][a t^2, t, s]; ft = Inactive[FourierTransform][a f[t], t, \[Omega]]; conv = Inactive[Convolve][a f[t], g[t], t, s];

As derivadas de todos eles no que diz respeito ao último argumento podem ser expressas em termos do próprio operador integral.

In[2]:=

X D[lt, s]

Out[2]=

In[3]:=

X D[ft, \[Omega]]

Out[3]=

In[4]:=

X D[conv, s]

Out[4]=

Em todos eles, 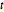é uma variável dummy, assim derivadas em relação a ele são zero.

In[5]:=

X D[lt, t]

Out[5]=

In[6]:=

X D[ft, t]

Out[6]=

In[7]:=

X D[conv, t]

Out[7]=

Todas as transformadas são lineares, então as derivadas com respeito aos parâmetros podem ser realizadas.

In[8]:=

X D[lt, a]

Out[8]=

In[9]:=

X D[ft, a]

Out[9]=

In[10]:=

X D[conv, a]

Out[10]=