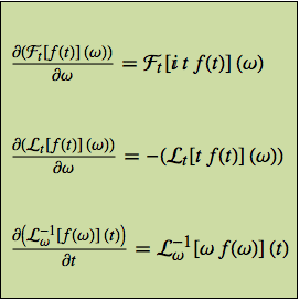Compute with Integral Transforms
Properties of integral and other formal operators are applied to their inactive forms.
Integral operators include LaplaceTransform, FourierTransform, and Convolve.
| In[1]:= |  X |
The derivatives of all of these with respect to the last argument can be expressed in terms of the integral operator itself.
| In[2]:= | X |
| Out[2]= |
| In[3]:= | X |
| Out[3]= |
| In[4]:= | X |
| Out[4]= |
In all of these, 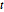 is a dummy variable, so derivatives with respect to it are zero.
is a dummy variable, so derivatives with respect to it are zero.
| In[5]:= | X |
| Out[5]= |
| In[6]:= | X |
| Out[6]= |
| In[7]:= | X |
| Out[7]= |
All of the transforms are linear, so derivatives with respect to parameters can simply be performed.
| In[8]:= | X |
| Out[8]= |
| In[9]:= | X |
| Out[9]= |
| In[10]:= | X |
| Out[10]= |