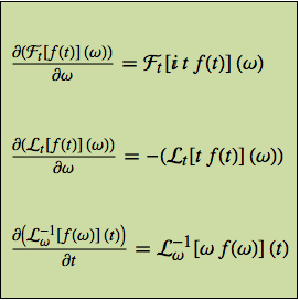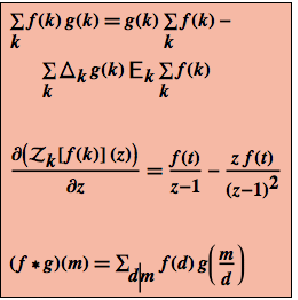Calcule con transformadas integrales
Las propiedades de integrales y otros operadores formales son aplicados a sus formas inactivas.
Los operadores integrales incluyen: LaplaceTransform, FourierTransform y Convolve.
| In[1]:= |  X |
Las derivadas de todos estos con respecto a su último argumento pueden ser expresadas en términos del operador integral mismo.
| In[2]:= |  X |
| Out[2]= |  |
| In[3]:= |  X |
| Out[3]= |  |
| In[4]:= |  X |
| Out[4]= |  |
En todos estos,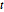 
es una variable ficticia, así que las derivadas con respecto a ésta son cero.
| In[5]:= |  X |
| Out[5]= |  |
| In[6]:= |  X |
| Out[6]= |  |
| In[7]:= |  X |
| Out[7]= |  |
Todas las transformadas son lineales, así que las derivadas con respecto a los parámetros pueden ser realizadas fácilmente.
| In[8]:= |  X |
| Out[8]= |  |
| In[9]:= |  X |
| Out[9]= |  |
| In[10]:= |  X |
| Out[10]= |  |
