偏微分方程式とイベント
さまざまな形の皿の縁が熱せられた後,その中心がある温度に到達するまでの時間を判定する.
| In[1]:= |  X |
皿の中心が 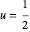 に到達したら積分を中止しその時間を記録する.境界の解が一貫性のない初期条件0から指定された境界条件1に非常に素早く近付くように,スケール因子103のオプションが使われる.
に到達したら積分を中止しその時間を記録する.境界の解が一貫性のない初期条件0から指定された境界条件1に非常に素早く近付くように,スケール因子103のオプションが使われる.
| In[2]:= |  X |
| Out[2]= |
中心が 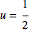 に到達した時間におけるそれぞれの解を表示する.
に到達した時間におけるそれぞれの解を表示する.
| In[3]:= |  X |
| Out[3]= | 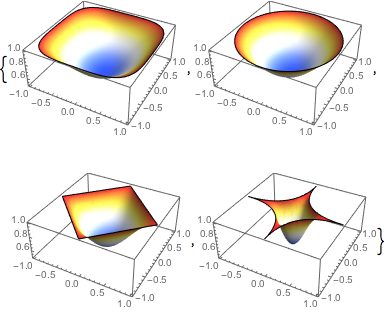 |
さまざまな形の皿の縁が熱せられた後,その中心がある温度に到達するまでの時間を判定する.
| In[1]:= |  X |
皿の中心が 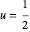 に到達したら積分を中止しその時間を記録する.境界の解が一貫性のない初期条件0から指定された境界条件1に非常に素早く近付くように,スケール因子103のオプションが使われる.
に到達したら積分を中止しその時間を記録する.境界の解が一貫性のない初期条件0から指定された境界条件1に非常に素早く近付くように,スケール因子103のオプションが使われる.
| In[2]:= |  X |
| Out[2]= |
中心が 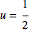 に到達した時間におけるそれぞれの解を表示する.
に到達した時間におけるそれぞれの解を表示する.
| In[3]:= |  X |
| Out[3]= |  |
Questions? Comments? Contact a Wolfram expert »