Solve PDEs with Material Regions 

Solve an electrostatics PDE over a region with two materials.

Specify a mesh.

In[1]:=

X bmesh = MeshRegion[{{0., 0.}, {1., 0.}, {1., 0.2}, {1., 1.}, {0., 1.}, {0., 0.22}, {0.3, 0.22}, {0.3, 0.2}, {0., 0.2}}, {Line[{{1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 6}, {6, 7}, {7, 8}, {8, 9}, {9, 1}, {3, 8}}]}]

Out[1]=

Solve the equation with material coefficients specified with an If statement.

In[2]:=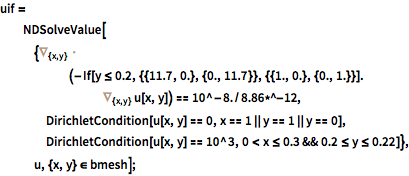

X uif = NDSolveValue[{Inactive[ Div][(-If[ y <= 0.2, {{11.7, 0.}, {0., 11.7}}, {{1., 0.}, {0., 1.}}].Inactive[Grad][u[x, y], {x, y}]), {x, y}] == 10^-8./8.86*^-12, DirichletCondition[u[x, y] == 0, x == 1 || y == 1 || y == 0], DirichletCondition[u[x, y] == 10^3, 0 < x <= 0.3 && 0.2 <= y <= 0.22]}, u, {x, y} \[Element] bmesh];

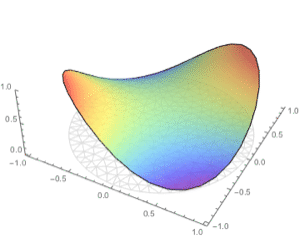
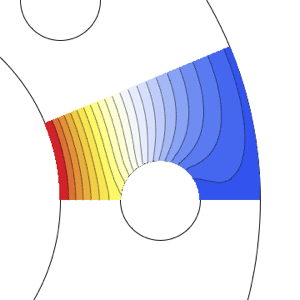
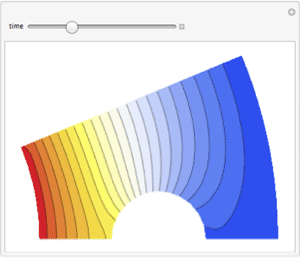
Contour plot the solution with the boundary mesh.

In[3]:=

X Show[ContourPlot[uif[x, y], {x, y} \[Element] uif["ElementMesh"], ColorFunction -> "TemperatureMap"], bmesh]

Out[3]=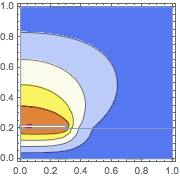