Neumann Values
Compute the cooling effect of a duct with a cooling liquid in an axisymmetric cross section of a pipe.
Neumann values prescribe the flux over the boundary edge.
| In[1]:= | 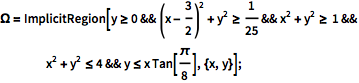 X |
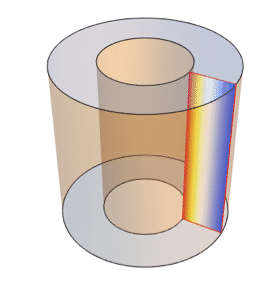
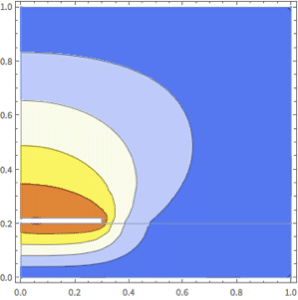
Visualize the simulation region.
| Out[2]= | 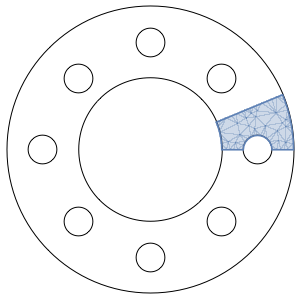 |
Specify Dirichlet boundary conditions to set temperatures inside the pipe and outside.
| In[3]:= | X |
Specify a flux into the cooling duct in the pipe.
| In[4]:= | X |
Solve the Laplace equation.
| In[5]:= | X |
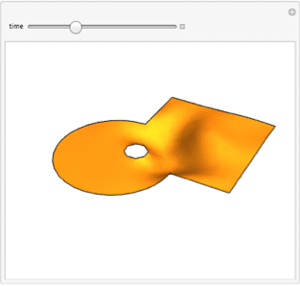
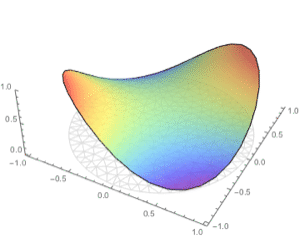
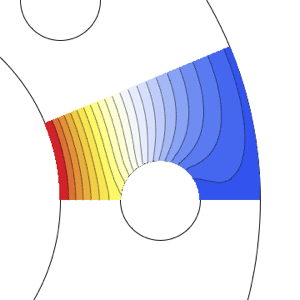
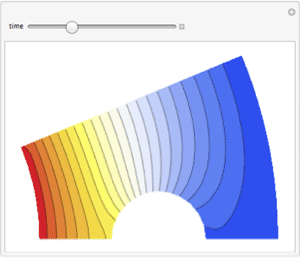
Plot the solution.
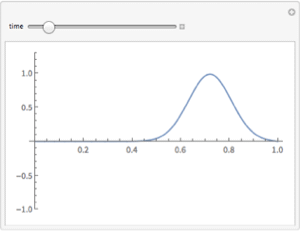
| In[6]:= |  X |
| Out[6]= | 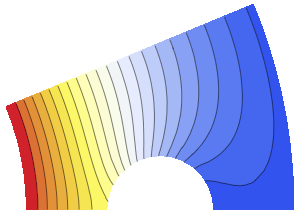 |
| Out[7]= | 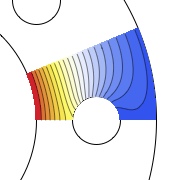 |