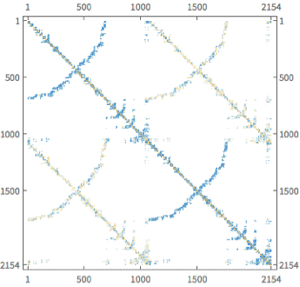
Solve Axisymmetric PDEs 

Solve a PDE over a axisymmetric region.

In[1]:=

X Subscript[r, 1] = 1; Subscript[r, 2] = 2; \[CapitalOmega] = ImplicitRegion[ True, {{r, Subscript[r, 1], Subscript[r, 2]}, {z, 0, 1/2}}];

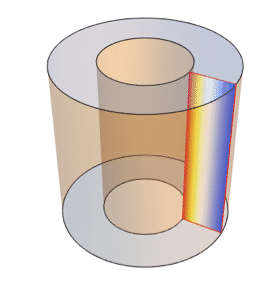
Specify a Neumann value of 100 W/m²(watt per square meter) at the inner edge and a temperature of 10 °C (degrees) at the outer edge, with a thermal conduction coefficient k of 10 W/m/C (watt per meter per degree).

In[2]:=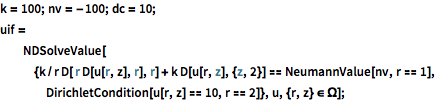

X k = 100; nv = -100; dc = 10; uif = NDSolveValue[{k/r D[ r D[u[r, z], r], r] + k D[u[r, z], {z, 2}] == NeumannValue[nv, r == 1], DirichletCondition[u[r, z] == 10, r == 2]}, u, {r, z} \[Element] \[CapitalOmega]];

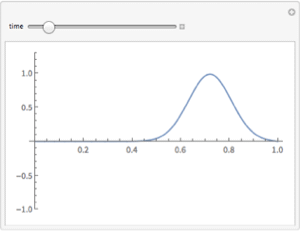
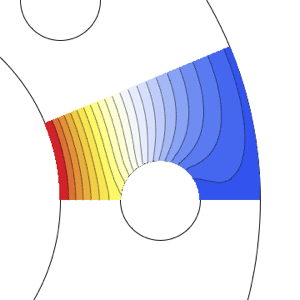
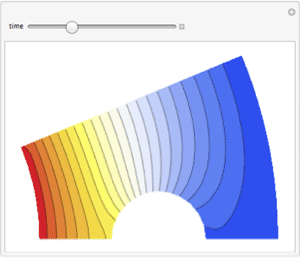
Plot the solution.

In[3]:=

X dp = DensityPlot[uif[r, z], {r, z} \[Element] \[CapitalOmega], ColorFunction -> "Temperature"]

Out[3]=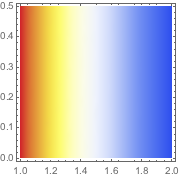

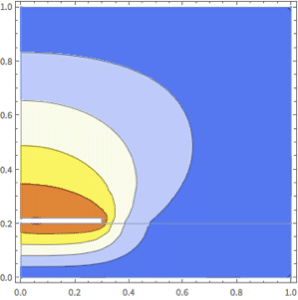
Verify the solution.

In[4]:=

X analyticalSolution[r_, z_] = (dc + nv*Subscript[r, 1]/k Log[r/Subscript[r, 2]]); Plot[uif[r, 0] - analyticalSolution[r, z], {r, Subscript[r, 1], Subscript[r, 2]}]

Out[4]=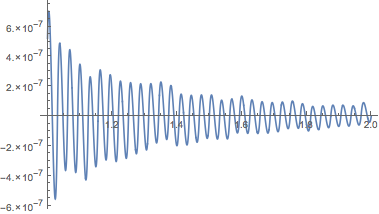

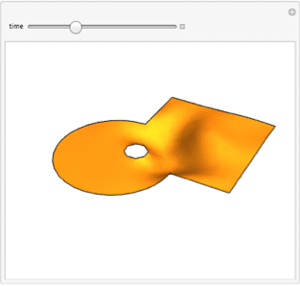
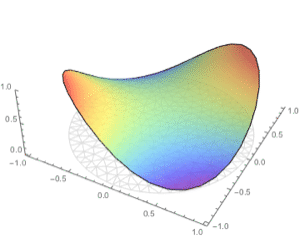
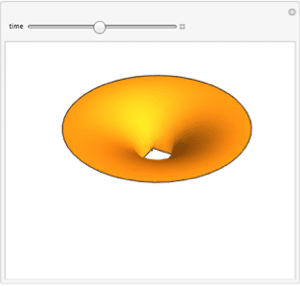
Plot the solution in 3D.

show complete Wolfram Language inputhide input

In[5]:=

X Show[ RegionPlot3D[ 1 <= x^2 + y^2 <= 4 && 0 <= z <= 1/2, {x, -2, 2}, {y, -2, 2}, {z, 0, 1/2}, Boxed -> False, Axes -> False, PlotPoints -> 40, PlotStyle -> {Opacity[0.2]}, Mesh -> False], Graphics3D[{EdgeForm[Red], FaceForm[Gray], GraphicsComplex[{{1, 0, 0}, {2, 0, 0}, {2, 0, 1/2}, {1, 0, 1/2}}, {Texture[ Show[dp, Frame -> False, PlotRangePadding -> None]], Lighting -> {{"Ambient", White}}, Polygon[{{1, 2, 3, 4}}, VertexTextureCoordinates -> {{{0, 0}, {1, 0}, {1, 1}, {0, 1}}}]}]}] ]

Out[5]=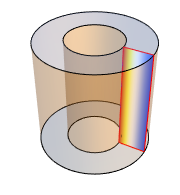