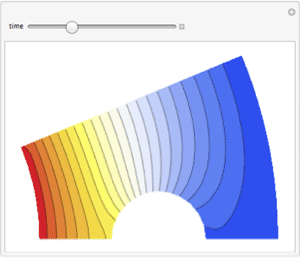
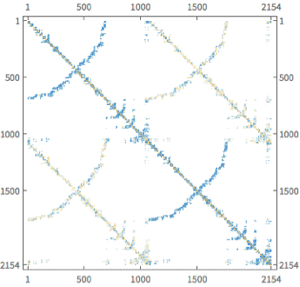
Transient Neumann Values 

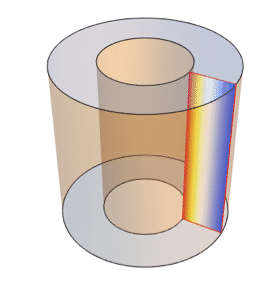
Compute the cooling effect of a duct with a cooling liquid in an axisymmetric cross section of a pipe.

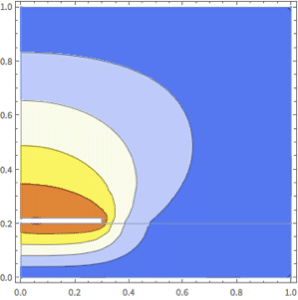
Specify a solution domain.

In[1]:=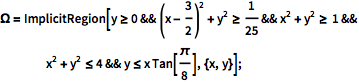

X \[CapitalOmega] = ImplicitRegion[ y >= 0 && (x - 3/2)^2 + y^2 >= 1/25 && x^2 + y^2 >= 1 && x^2 + y^2 <= 4 && y <= x Tan[\[Pi]/8], {x, y}];

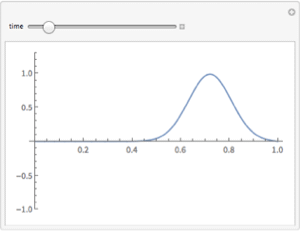
Specify a Neumann value that depends on time and stationary Dirichlet conditions.

In[2]:=

X Subscript[\[CapitalGamma], N][t_] = NeumannValue[ If[t <= 10., -100. t, -1000.], (x - 3/2)^2 + y^2 == 1/25];

In[3]:=

X Subscript[\[CapitalGamma], D][ t_] = {DirichletCondition[u[t, x, y] == 200., x^2 + y^2 == 1], DirichletCondition[u[t, x, y] == 15., x^2 + y^2 == 4]};

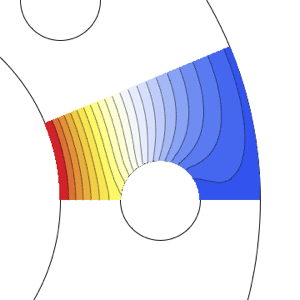
Solve a steady-state problem corresponding to the boundary conditions at 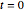to find an initial condition. The "Continuation" mesh generator is used to better resolve the corners and edges of the domain .

In[4]:=

X uinit = NDSolveValue[{10 \!\( \*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[0, x, y]\)\) == 0, Subscript[\[CapitalGamma], D][0]}, u[0, x, y], {x, y} \[Element] \[CapitalOmega], Method -> {"PDEDiscretization" -> {"FiniteElement", "MeshOptions" -> {"BoundaryMeshGenerator" -> "Continuation"}}}];

Solve a heat equation with a temperature set on the outer boundaries and a time-dependent flux over the inner boundary, using the steady-state solution as an initial condition. To ensure the best initialization, the same spatial mesh is used as for the steady-state solution.

In[5]:=

X uif = NDSolveValue[{D[u[t, x, y], t] - 10 \!\( \*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[t, x, y]\)\) == Subscript[\[CapitalGamma], N][t], Subscript[\[CapitalGamma], D][0], u[0, x, y] == uinit}, u, {t, 0, 25}, {x, y} \[Element] Head[uinit]["ElementMesh"]];

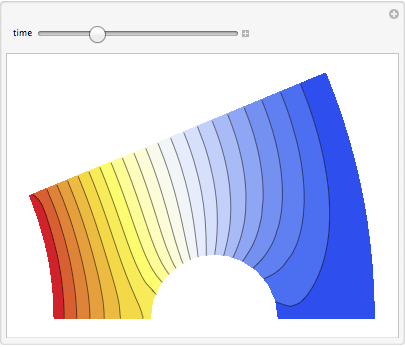
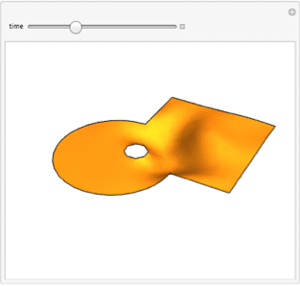
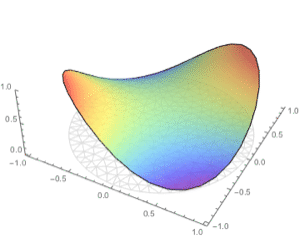
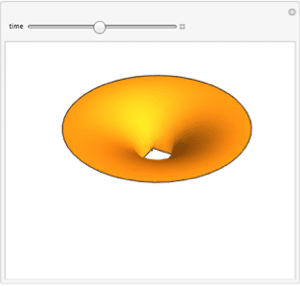
Plot the solution.

show complete Wolfram Language inputhide input

In[6]:=

X framesNTV = Table[ContourPlot[ uif[t, x, y], {x, y} \[Element] uif["ElementMesh"], Mesh -> None, ColorFunction -> "TemperatureMap", Contours -> 21, PlotRange -> All, AspectRatio -> Automatic, Frame -> False], {t, 1/2, 15, 1/2}];

In[7]:=

X Manipulate[framesNTV[[i]], {{i, 9, "time"}, 1, Length[framesNTV], 1}, SaveDefinitions -> True]

Out[7]=

Play Animation Stop Animation