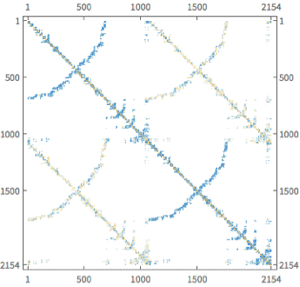
PDEs and Events 

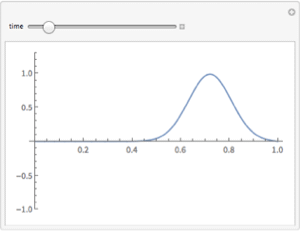
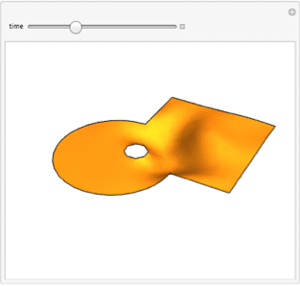
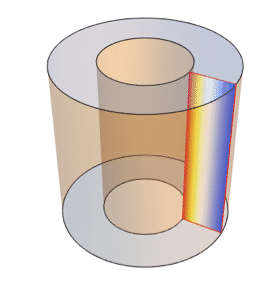
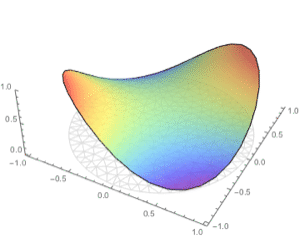
Determine the time for the centers of differently shaped plates to reach a certain temperature after the edges are heated.

In[1]:=

X Subscript[\[CapitalOmega], 1] = ImplicitRegion[x^4 + y^4 <= 1, {x, y}]; Subscript[\[CapitalOmega], 2] = ImplicitRegion[x^2 + y^2 <= 1, {x, y}]; Subscript[\[CapitalOmega], 3] = ImplicitRegion[Abs[x] + Abs[y] <= 1, {x, y}]; Subscript[\[CapitalOmega], 4] = ImplicitRegion[Sqrt[Abs[x]] + Sqrt[Abs[y]] <= 1, {x, y}];

Stop integration and record the time when the plate center reaches 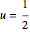. The scale factor of 10³ option is used so that the solution at the boundaries approaches the specified boundary condition of 1 very quickly from the (inconsistent) initial condition of 0.

In[2]:=

X Table[uhsol[i] = NDSolveValue[{\!\( \*SubscriptBox[\(\[PartialD]\), \(t\)]\(u[t, x, y]\)\) == Inactive[Laplacian][u[t, x, y], {x, y}], DirichletCondition[u[t, x, y] == 1, True], u[0, x, y] == 0, WhenEvent[ u[t, 0, 0] == 1/2, {Subscript[T, i] = t, "StopIntegration"}]}, u, {t, 0, 1}, {x, y} \[Element] Subscript[\[CapitalOmega], i], Method -> {"PDEDiscretization" -> {"MethodOfLines", "DifferentiateBoundaryConditions" -> {True, "ScaleFactor" -> 10^3}}}]; Subscript[T, i], {i, 1, 4}]

Out[2]=

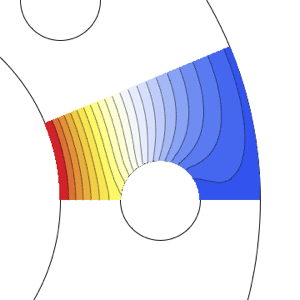
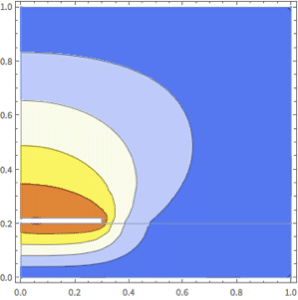
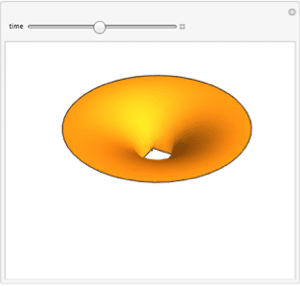
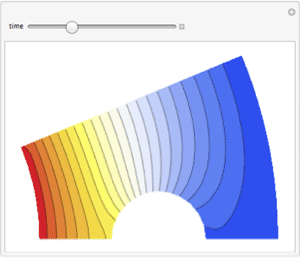
Show each of the solutions at the time where the center has reached .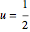

In[3]:=

X Table[Plot3D[ uhsol[i][Subscript[T, i], x, y], {x, y} \[Element] uhsol[i]["ElementMesh"], PlotPoints -> 40, Mesh -> None, ColorFunction -> "TemperatureMap"], {i, 4}]

Out[3]=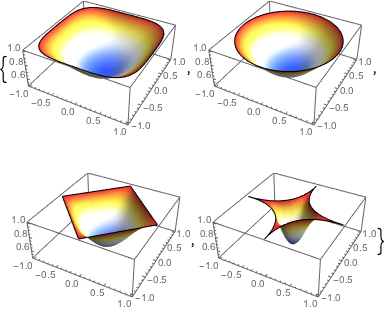