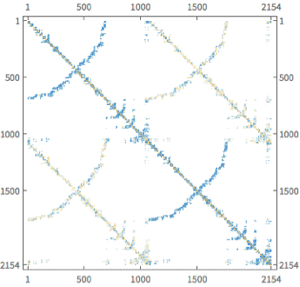
Compute a Plane Strain Deformation 

Define a plane strain operator.

In[1]:=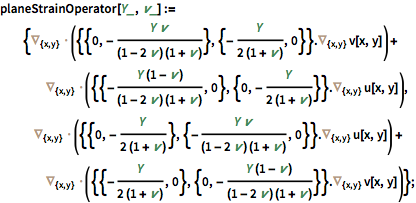

X planeStrainOperator[ Y_, \[Nu]_] := {Inactive[ Div][({{0, -((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu])))}, {-(Y/( 2 (1 + \[Nu]))), 0}}.Inactive[Grad][v[x, y], {x, y}]), {x, y}] + Inactive[ Div][({{-((Y (1 - \[Nu]))/((1 - 2 \[Nu]) (1 + \[Nu]))), 0}, {0, -(Y/(2 (1 + \[Nu])))}}.Inactive[Grad][ u[x, y], {x, y}]), {x, y}], Inactive[ Div][({{0, -(Y/(2 (1 + \[Nu])))}, {-(( Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu]))), 0}}.Inactive[Grad][ u[x, y], {x, y}]), {x, y}] + Inactive[ Div][({{-(Y/(2 (1 + \[Nu]))), 0}, {0, -(( Y (1 - \[Nu]))/((1 - 2 \[Nu]) (1 + \[Nu])))}}.Inactive[ Grad][v[x, y], {x, y}]), {x, y}]};

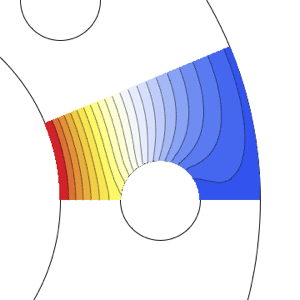
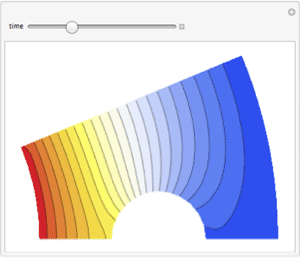
Solve the equation over a rectangular region. On the left-hand side both dependent variables are held fixed with 0 displacement and on the right-hand side with a boundary load of one unit in the direction of negative y axes.

In[2]:=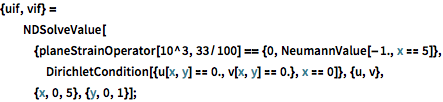

X {uif, vif} = NDSolveValue[{planeStrainOperator[10^3, 33/100] == {0, NeumannValue[-1., x == 5]}, DirichletCondition[{u[x, y] == 0., v[x, y] == 0.}, x == 0]}, {u, v}, {x, 0, 5}, {y, 0, 1}];

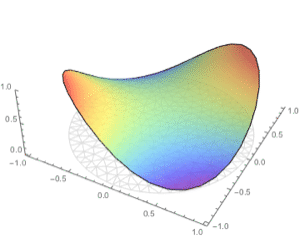
Visualize the deformation in the x and y directions using the finite element package.

show complete Wolfram Language inputhide input

In[3]:=

X Needs["NDSolve`FEM`"] mesh = uif["ElementMesh"]; Show[{ mesh["Wireframe"[ "MeshElement" -> "BoundaryElements"]], ElementMeshDeformation[mesh, {uif, vif}][ "Wireframe"[ "ElementMeshDirective" -> Directive[EdgeForm[Red], FaceForm[]]]]}, ImageSize -> 300]

Out[3]=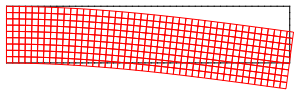