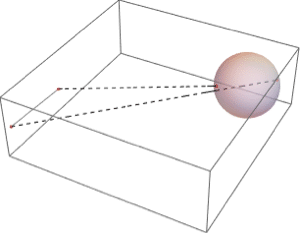
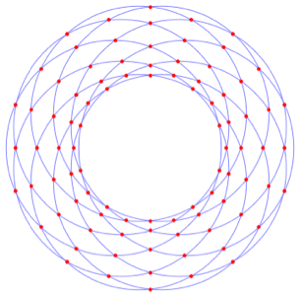
数式定義領域 

数式定義領域は陰的条件の論理結合を使ったImplicitRegionか，いくつかのパラメータの明示的パラメトリック関数を使ったParametricRegionにより定義される．数式定義領域は領域の数学的定義を与える柔軟な方法を提供し，どの幾何学的次元の領域も定義でき，どの次元にでも埋め込むことができる．

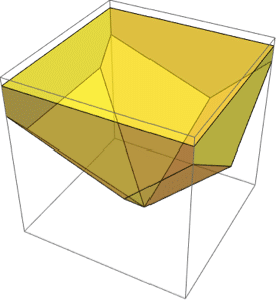
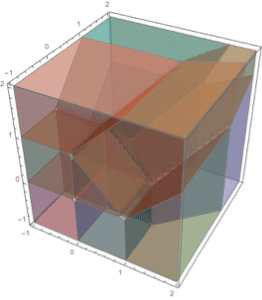
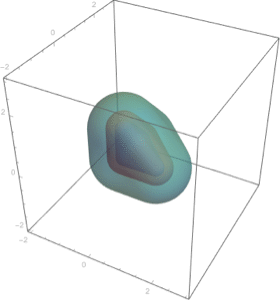
陰的条件の論理結合により定義された領域．

In[1]:=

X \[ScriptCapitalR] = ImplicitRegion[1 <= x^2 + y^2 <= 2, {x, y}];

In[2]:=

X RegionPlot[\[ScriptCapitalR], FrameTicks -> None]

Out[2]=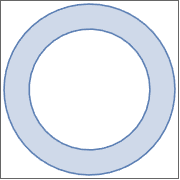

In[3]:=

X Integrate[1, x \[Element] \[ScriptCapitalR]]

Out[3]=

In[4]:=

X \[ScriptCapitalR] = ImplicitRegion[x y z <= 1, {{x, -5, 5}, {y, -5, 5}, {z, -5, 5}}];

In[5]:=

X RegionPlot3D[\[ScriptCapitalR], PlotStyle -> Opacity[0.5]]

Out[5]=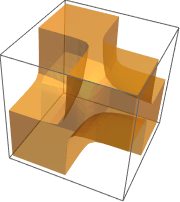

In[6]:=

X Integrate[1, x \[Element] \[ScriptCapitalR]]

Out[6]=

In[7]:=

X \[ScriptCapitalR] = ImplicitRegion[-1 + (-1 + 18 x^2 - 48 x^4 + 32 x^6)^2 + (-1 + 18 y^2 - 48 y^4 + 32 y^6)^2 <= 0, {x, y}];

In[8]:=

X RegionPlot[\[ScriptCapitalR], FrameTicks -> None] // Quiet

Out[8]=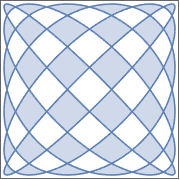

明示的パラメトリック関数により定義された領域．

In[9]:=

X \[ScriptCapitalR] = ParametricRegion[{Cos[\[Theta]], Sin[\[Theta]]}, {{\[Theta], 0, 2 \[Pi]}}];

In[10]:=

X RegionPlot[\[ScriptCapitalR], FrameTicks -> None]

Out[10]=

In[11]:=

X \[ScriptCapitalR] = ParametricRegion[{{s^2 t^2, s t^3}, -1 <= s <= 1 && -1 <= t <= 1}, {s, t}];

In[12]:=

X RegionPlot[\[ScriptCapitalR], FrameTicks -> None]

Out[12]=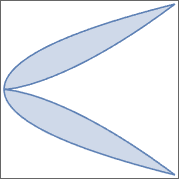