Über Regionen integrieren
Integrieren Sie über einer beliebigen Region. Das Integral, das verwendet wird, hängt von der Dimension der Region ab: Ein Kurvenintegral für eindimensionale Integrale, ein Flächenintegral für zweidimensionale Regionen etc. Integrale können symbolisch oder numerisch berechnet werden.
Die Kurvenlänge ist ein Integral über einer Kurve.
| In[1]:= | X |
| Out[1]= |
| In[2]:= | X |
| Out[2]= |
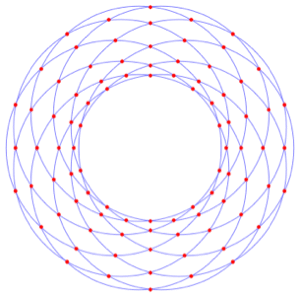
Der Flächeninhalt ist ein Integral über einer Fläche.
| In[3]:= | X |
| Out[3]= |
| In[4]:= | X |
| Out[4]= |
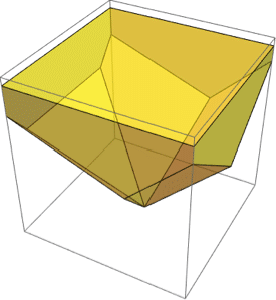
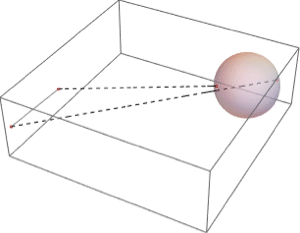
Das Volumen ist ein Integral über einem geometrischen Körper.
| In[5]:= | X |
| Out[5]= |
| In[6]:= | X |
| Out[6]= |
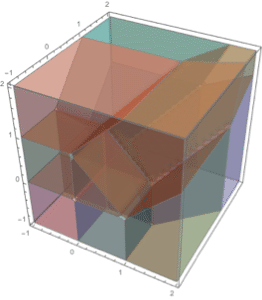
Integrieren Sie in jeder beliebigen Anzahl von Dimensionen.
| In[7]:= | X |
| Out[7]= |
Verwenden Sie symbolische Vektorvariablen.
| In[8]:= | X |
| Out[8]= |
| In[9]:= | X |
| Out[9]= |
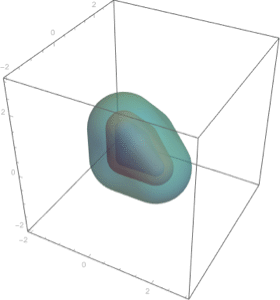
Integrieren Sie über jeder beliebigen Region.
| In[10]:= | 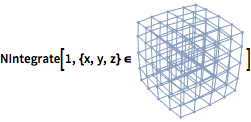 X |
| Out[10]= |
| In[11]:= | 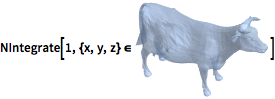 X |
| Out[11]= |
| In[12]:= | 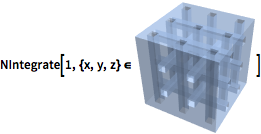 X |
| Out[12]= |