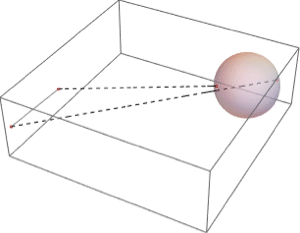
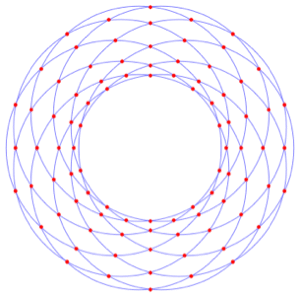
領域上の積分
任意の領域上で積分する.使用される実際の積分は一次元積分には線積分が,二次元領域には面積分が使われるというように,領域の次元により異なる.積分は記号的にも数値的にも計算することができる.
曲線の長さは曲線上の積分である.
| In[1]:= | X |
| Out[1]= |
| In[2]:= | X |
| Out[2]= |
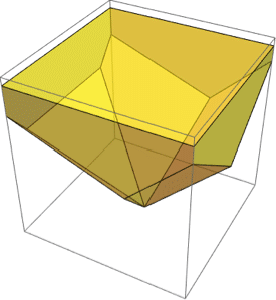
曲面の面積は曲面上の積分である.
| In[3]:= | X |
| Out[3]= |
| In[4]:= | X |
| Out[4]= |
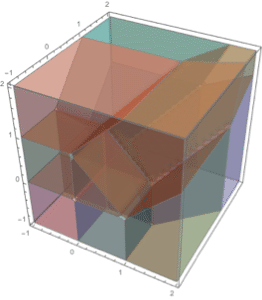
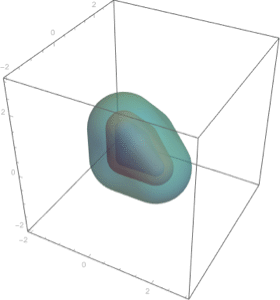
立体の体積は立体上の積分である.
| In[5]:= | X |
| Out[5]= |
| In[6]:= | X |
| Out[6]= |
何次元でも積分することができる.
| In[7]:= | X |
| Out[7]= |
記号的なベクトル変数を使う.
| In[8]:= | X |
| Out[8]= |
| In[9]:= | X |
| Out[9]= |
あらゆる領域上で積分する.
| In[10]:= | 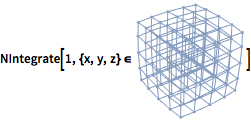 X |
| Out[10]= |
| In[11]:= | 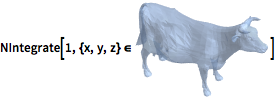 X |
| Out[11]= |
| In[12]:= | 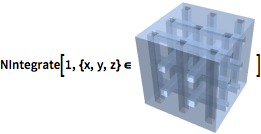 X |
| Out[12]= |